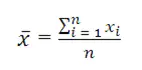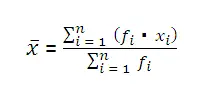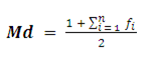10 ejemplos de Medidas de Tendencia Central
Las medidas de tendencia central son parámetros estadísticos que indican los valores medios de los datos estudiados, sean muestrales o poblacionales, agrupados o no. Se distinguen entre ellas la media o promedio, la mediana y el modo o moda.
Las medidas de tendencia central se encuentran en la mitad o centro del conjunto de los datos estadísticos que se desean analizar.
La estadística que trataremos acá se denomina Estadística Descriptiva.
Ejemplos de medidas de tendencia central
- La estatura promedio de los estudiantes de 3er grado es de 1,35 metros. [Media]
- La edad que más se repite en las niñas del coro es 11 años. [Moda]
- Una vez ordenados los datos, 17 es el valor que se ubica en la posición del medio de todos ellos. La parte de los datos se ubica antes de la mediana es de igual tamaño que la otra que se ubica después. [Mediana]
Medidas de Tendencia Central
Media
Conocida también como media aritmética o promedio. Es la media aritmética de los datos estudiados, la cual se obtiene sumando los puntajes y dividendo esta suma entre el número de puntajes.
Fórmula
Media Aritmética = x ̅
Número de datos = n
Datos = x1, x2, x3, …, xn
Ejemplos:
- Un grupo familiar de 5 personas tiene las siguientes edades: 18, 25, 62, 15 y 55
x ̅ = (15 + 18 + 25 + 55 + 62)/5 = 175/5 = 35
Por tanto, la edad promedio del grupo familiar es de 35 años
- Cantidades de plomo medidas en microgramos por metro cúbico (μg⁄m^3 ) en el aire : 5, 40; 1, 10; 0, 42; 0, 73; 0, 48; 1, 10
x ̅ = (0,42 + 0,48 + 0,73 + 1,10 + 1,10 + 5,40 )/6 = (9,23)/6 = 1,538333… = 1,5383 ̅
Por tanto, la contaminación media del aire es de
Moda
Conocida también como Modo. Es el parámetro que nos indica cual es el puntaje que más se repite entre todos los puntajes, el de más alta frecuencia.
Se simboliza con Mo
Dependiendo de los datos que se estén analizando podemos tener una población:
- Amodal: si no tiene Moda.
- Unimodal: con una única Moda.
- Bimodal: con dos Modas.
- Multimodal: con más de dos Modas.
Ejemplos:
- Un equipo escolar se conformó con varios estudiantes de diversos grados, sus edades eran: 15, 15, 14, 14, 15, 15, 15, 12, 12, 13, 13,13, 13, 13,13, 13, 13,13, 14, 14, 14, 12, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 12.
Tenemos 4 estudiantes de 12 años, 10 de 13 años, 18 de 14 años y 5 de 15 años.
Por tanto, la Moda es el valor que más se repite. Mo = 14 años.
- Si el lunes, una ama de casa, tomó 4 vasos de agua (250 ml por vaso de agua) y el martes una botella de 500 cc, el miércoles 5 vasos de agua y el resto de los días 1 litro de agua por día. Tenemos: 250, 250, 250, 250, 500, 250, 250, 250, 250, 250, 1 000, 1 000, 1 000, 1 000. [1 litro = 1 000 ml = 1 000 cc]
Tenemos 9 ingestas de 250 cc, una de 500 cc y 4 de 1 000 cc.
Por tanto, la Mo = 250 cc, que es el valor que más se repite.
Mediana
Es el parámetro que divide la lista de puntajes en dos partes de igual tamaño. Para calcularla se deben ordenar los datos y considerar dos posibilidades:
- Si la lista de los puntajes es impar, se toma como mediana el puntaje que toma la posición del medio en la lista ordenada.
- Si la lista de los puntajes es par, se toman los dos valores centrales de la lista, se suman y dividen entre dos, el valor resultante es la mediana.
Se simboliza con Md
Ejemplos:
- En el ejemplo de las edades mostrado anteriormente, tenemos 37 estudiantes y sus edades eran: 15, 15, 14, 14, 15, 15, 15, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 13, 14, 14, 14, 12, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 12
Los ordenamos: 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15.
Como son 37 valores en el medio se encuentra el valor en la posición 19° (el cual indicamos en rojo).
Por tanto, la Md = 14 años.
- Tomemos ahora las medidas de plomo en el aire, similar a un ejemplo anterior: 5, 40; 1, 10; 0, 42; 0, 73; 0, 48; 1, 10; 0, 66
Los ordenamos: 0, 42; 0, 48; 0, 66; 0, 73; 1, 10; 1, 10.
Como son seis valores, calculamos la media aritmética de los dos valores centrales: 0, 66; 0, 73.
(0, 66 + 0, 73)/2 = 0, 695
Por tanto, la mediana de la muestra Md = 0, 695 μg⁄m^3 de plomo en el aire.
Medidas de Tendencia Central con datos agrupados
Las definiciones de Media, Moda y Mediana se mantienen, solo que ahora los datos están agrupados en clases y se modifica la forma de calcularlos.
Media 
x_i = marca de clase [(cota inferior + cota superior) / 2]
f_i = frecuencia en cada clase
Ejemplo:
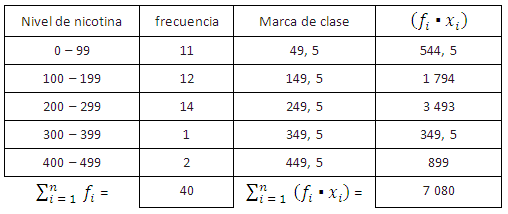
- A un grupo de 40 pacientes fumadores se les hace un estudio de sus niveles de nicotina:
Por tanto, el nivel promedio de nicotina de estos pacientes es x ̅ = 177
Moda
Mo = es la clase de mayor frecuencia.
Ejemplo:
Tomamos el mismo caso de los fumadores.
Por tanto, la clase modal es (200 – 299), por tanto, Mo = (200 – 299)
Mediana
Md = es la clase en la que se encuentra en el medio de la frecuencia acumulada.
Ejemplo:
| Nivel de nicotina | Frecuencia | Frecuencia acumulada |
|
0 – 99 |
11 | 11 |
|
100 – 199 |
12 | 23 |
|
200 – 299 |
14 |
37 |
| 300 – 399 | 1 |
38 |
|
400 – 499 |
2 |
40 |
| 40 |
|
Md = (1 + 40)/2 = 41/2 = 20,5
Este valor Md = 20, 5 se encuentra en la segunda clase (100 – 199)
Por tanto, la clase mediana es (100 – 199), Md = (100 – 199)
Ejercicios
- Determine la Moda (Mo) en los siguientes conjuntos de datos.
- 27 27 27 55 55 55 88 88 99
- 1 2 3 6 7 8 9 10
- Determine la Media en los siguientes conjuntos de datos:
- 15, 15, 14, 14, 15, 15, 15, 12, 14, 14, 14, 12, 13, 13, 13, 13, 14, 14, 14, 12, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 12, 13, 13, 13, 13, 13
- 250, 1 000, 250, 250, 250, 1 000, 250, 250, 1 000, 1 000, 250, 250, 500, 250
- Determine la media, moda y mediana en la siguiente tabla de datos agrupados:
| Edades | f | fa |
| 46 | 1 | 1 |
| 48 | 8 | 9 |
| 49 | 2 | 11 |
| 51 | 4 | 15 |
| 52 | 7 | 22 |
| 53 | 3 | 25 |
| 54 | 7 | 32 |
| 55 | 4 | 36 |
| 56 | 8 | 44 |
| 57 | 2 | 46 |
| 58 | 5 | 51 |
| 62 | 5 | 56 |
| 64 | 8 | 64 |
| 65 | 7 | 71 |
| 69 | 4 | 75 |
| 70 | 2 | 77 |
| 73 | 1 | 78 |
| 76 | 2 | 80 |
Pregunta
¿Habrá alguna diferencia si se calcula la media, moda y mediana con los datos sin agrupar con respecto a hacerlo con los datos agrupados?
Te invitamos a probarlo con base en este ejemplo: Un equipo escolar se conformó con varios estudiantes de diversos grados, sus edades eran: 15, 15, 14, 14, 15, 15, 15, 12, 12, 13, 13,13, 13, 13,13, 13, 13,13, 14, 14, 14, 12, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 12.
Para comprender e interpretar adecuadamente la información que nos suministran los datos, agrupados o no, debemos estudiar las medidas de tendencia central junto con las medidas de dispersión.
Ángel Míguez Álvarez