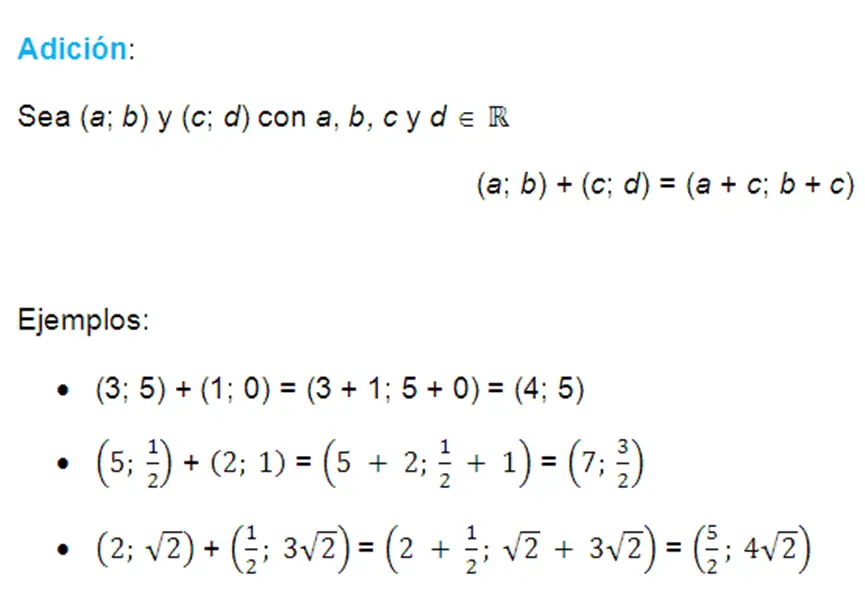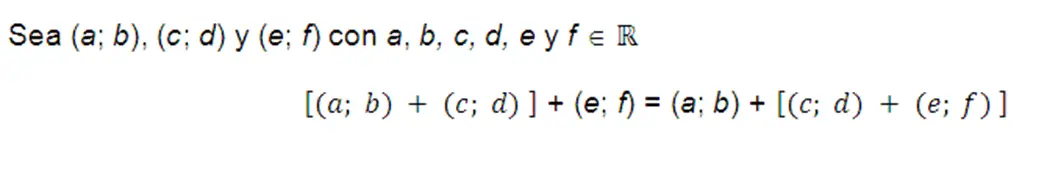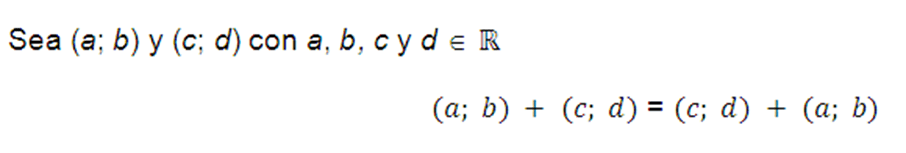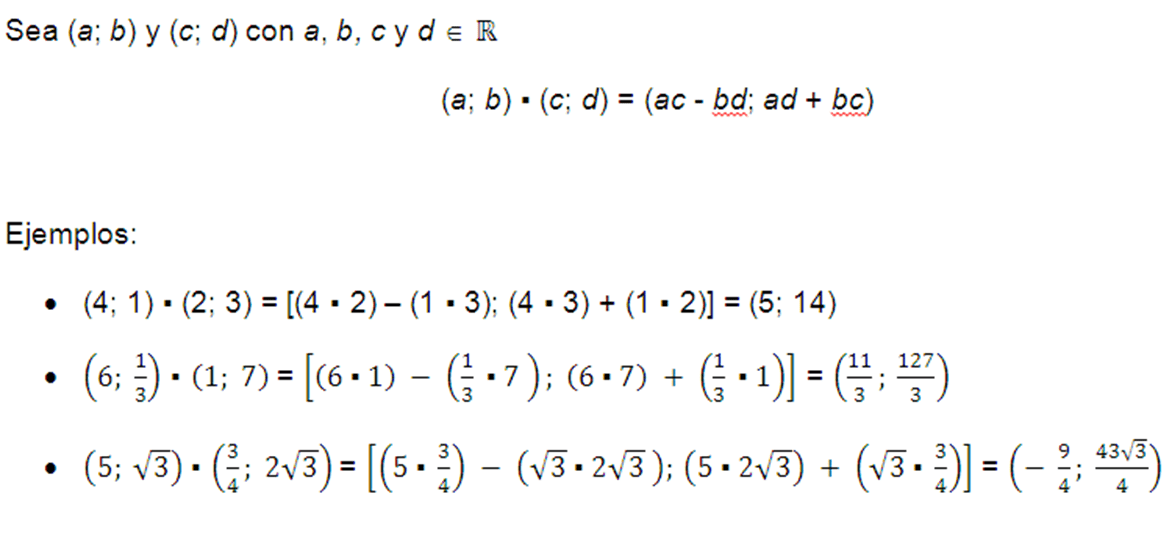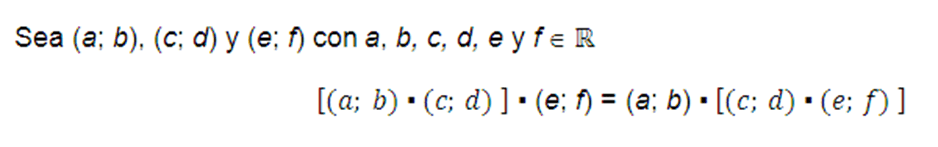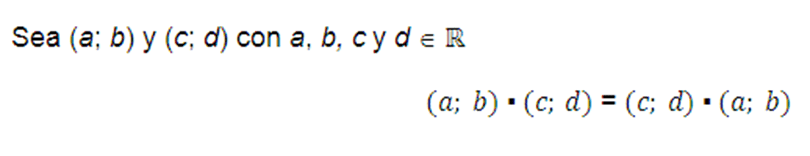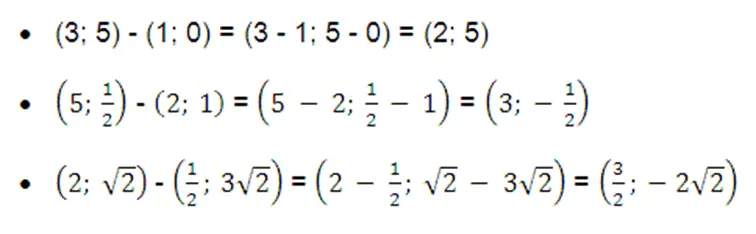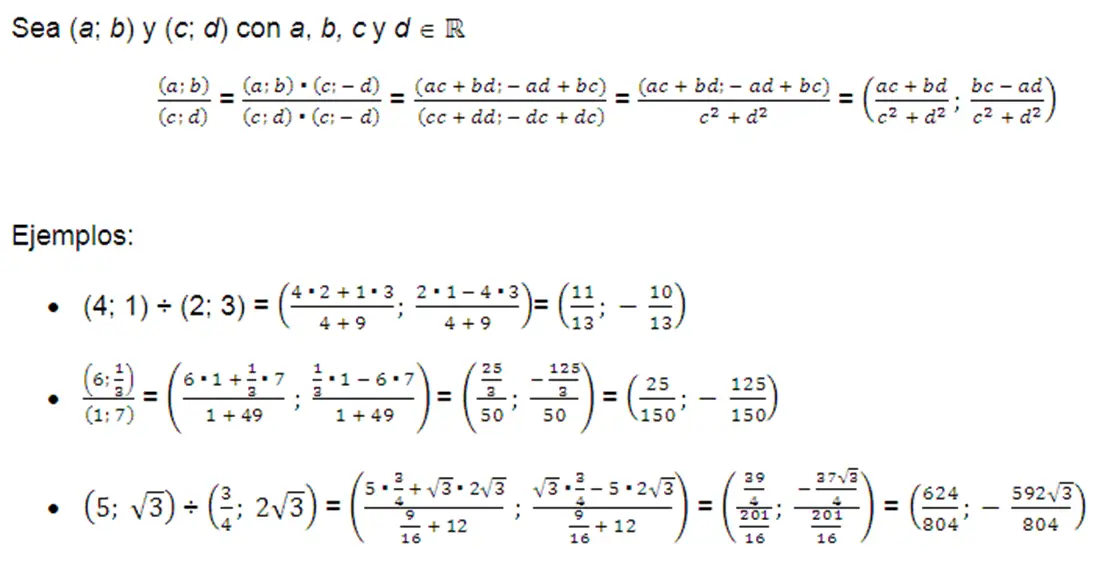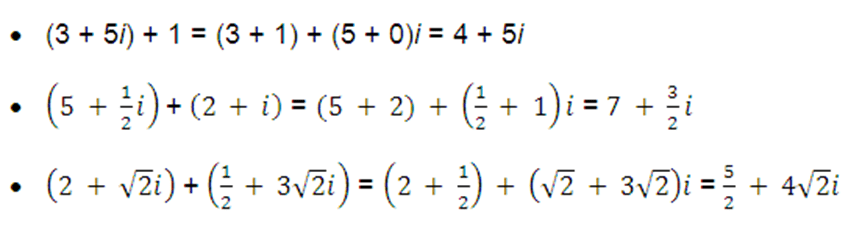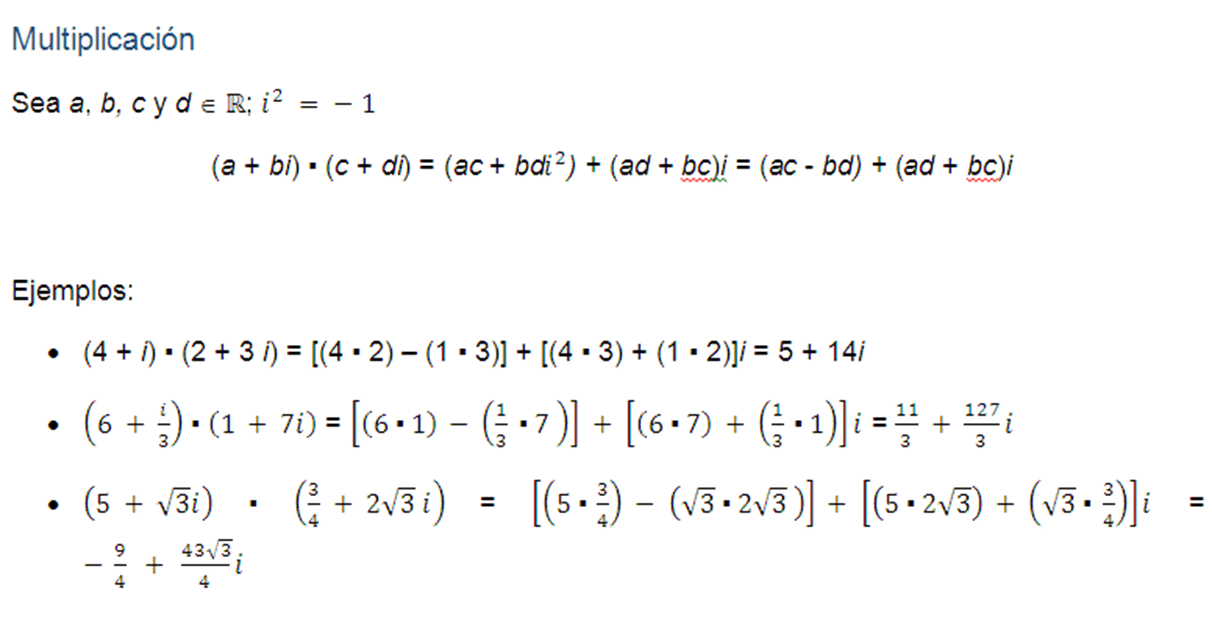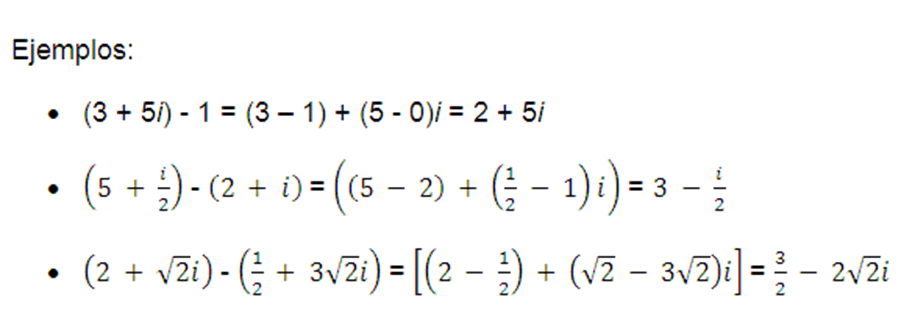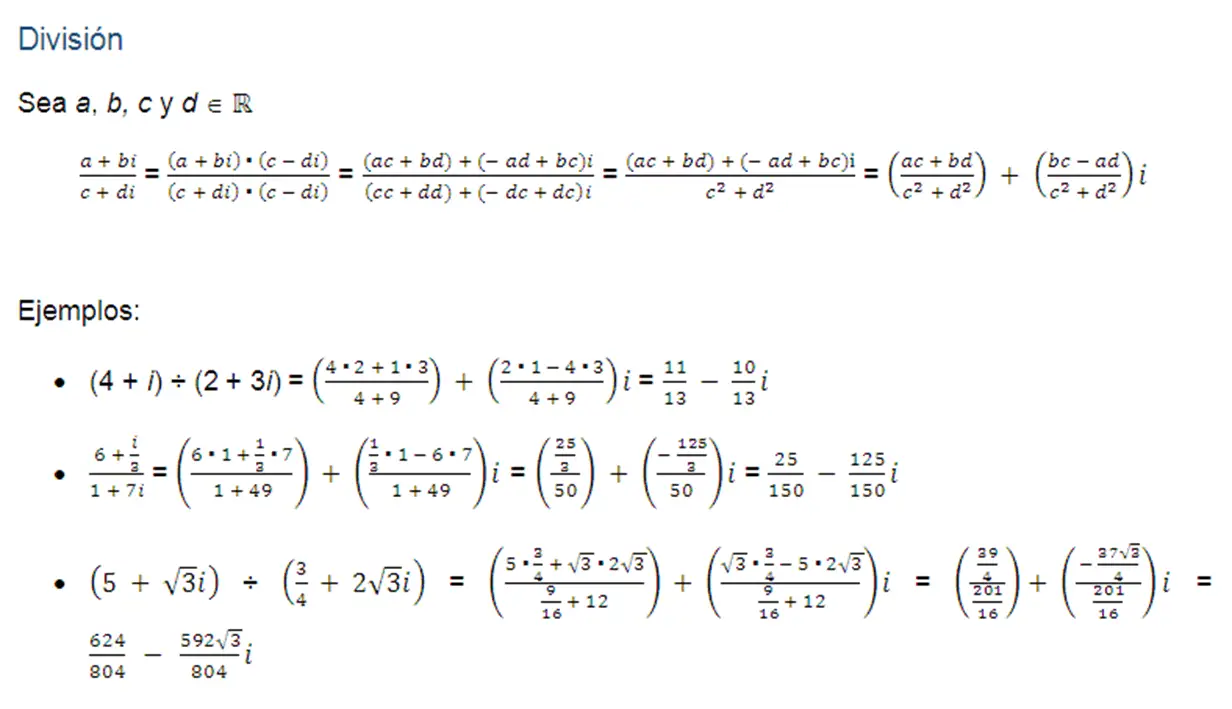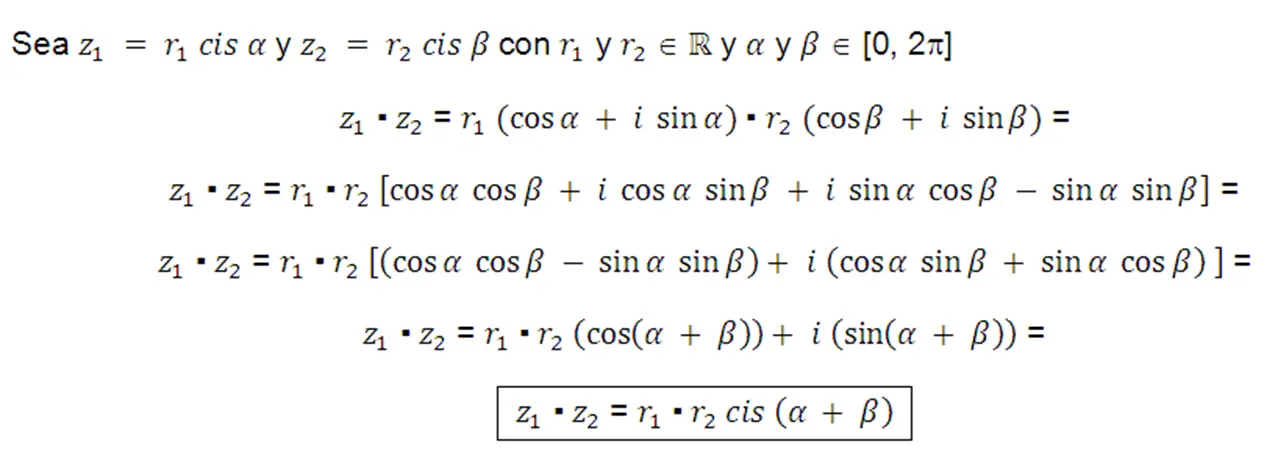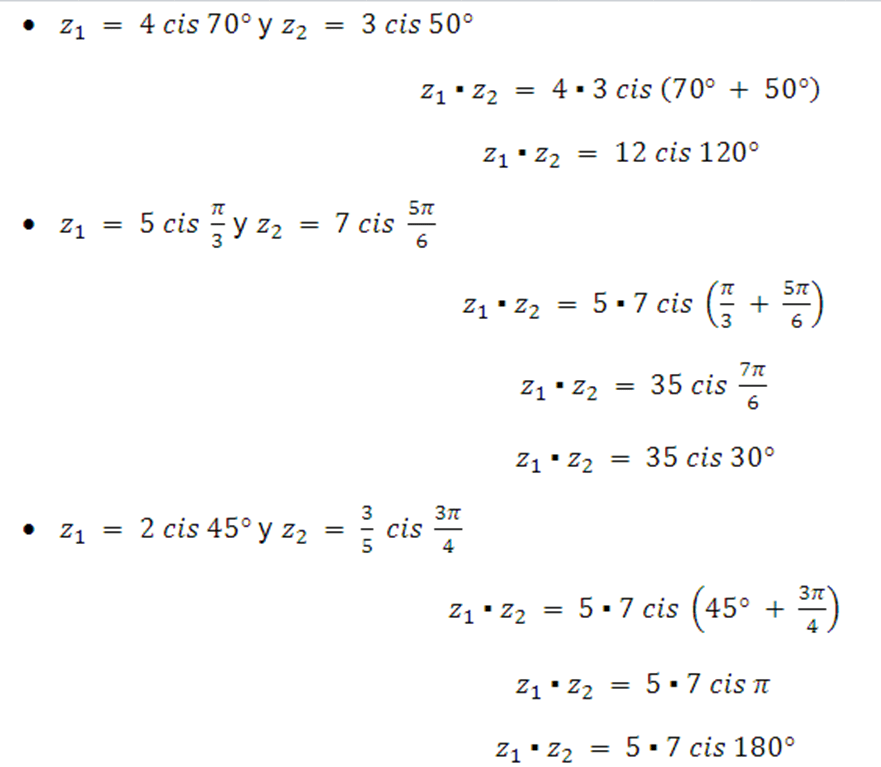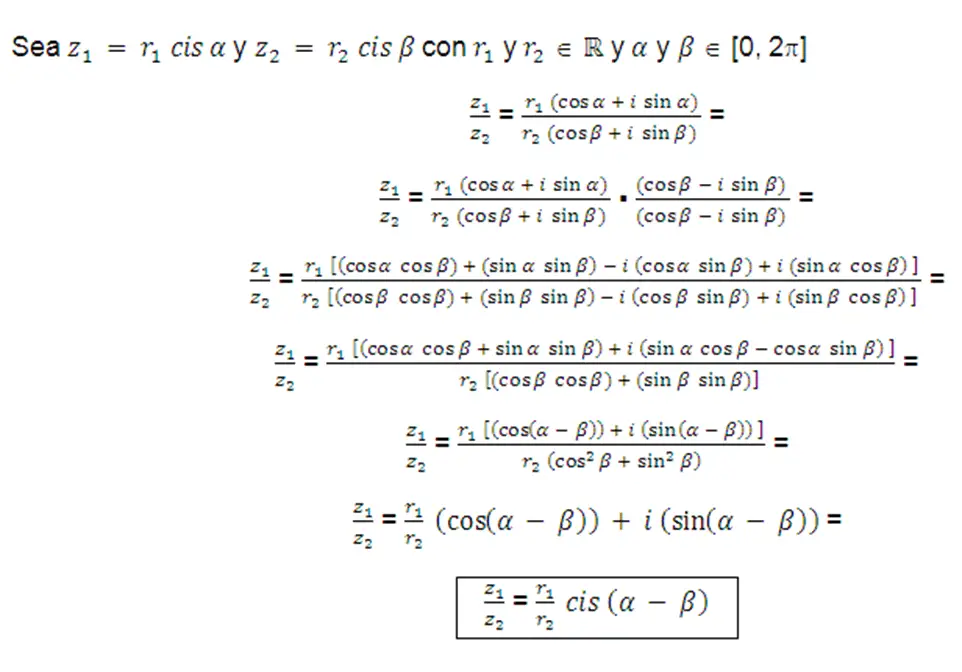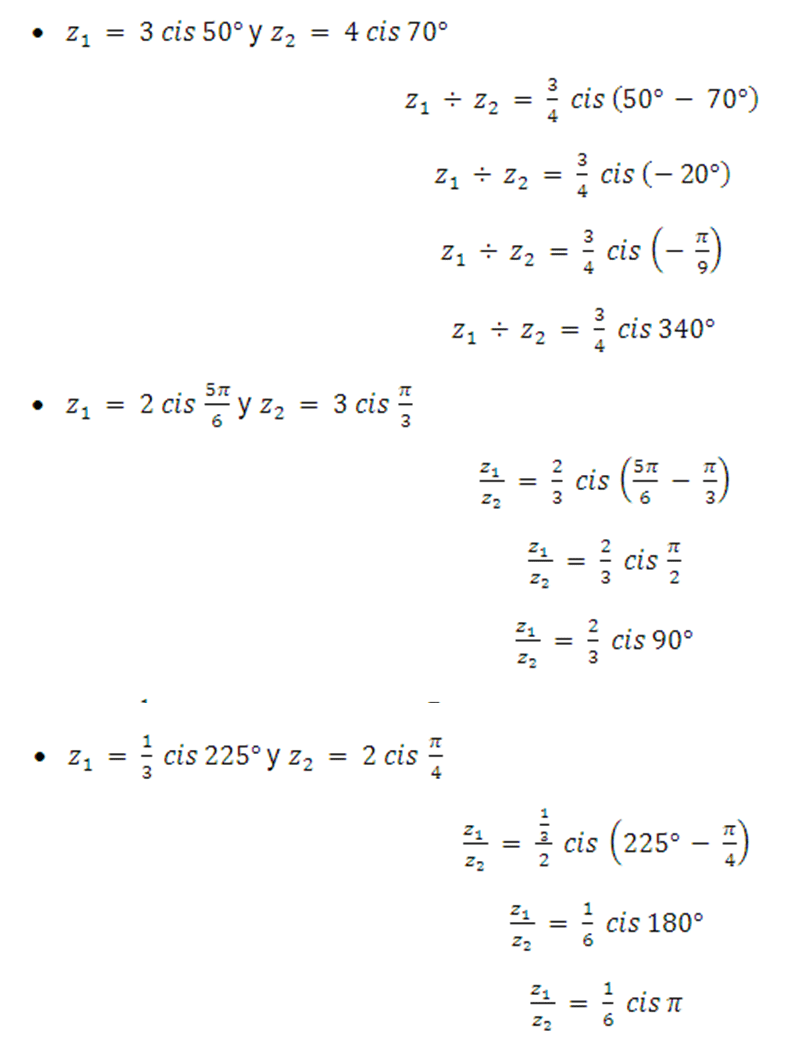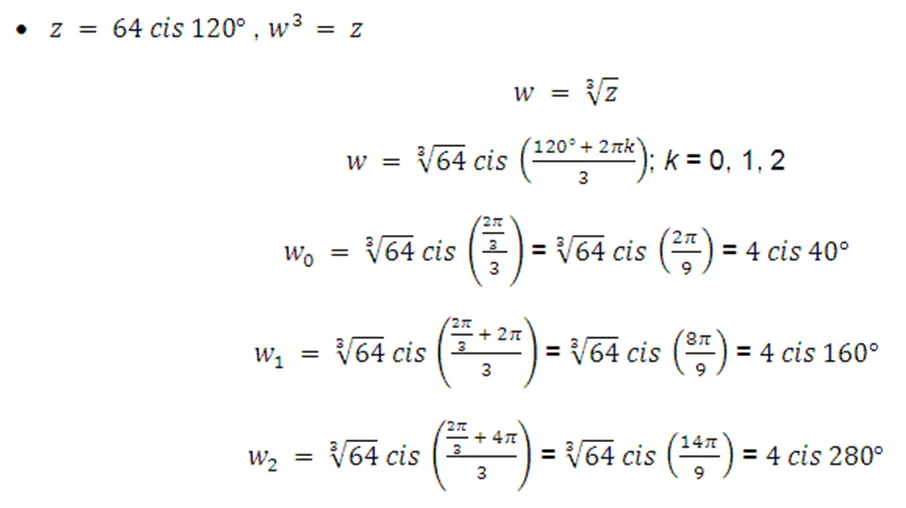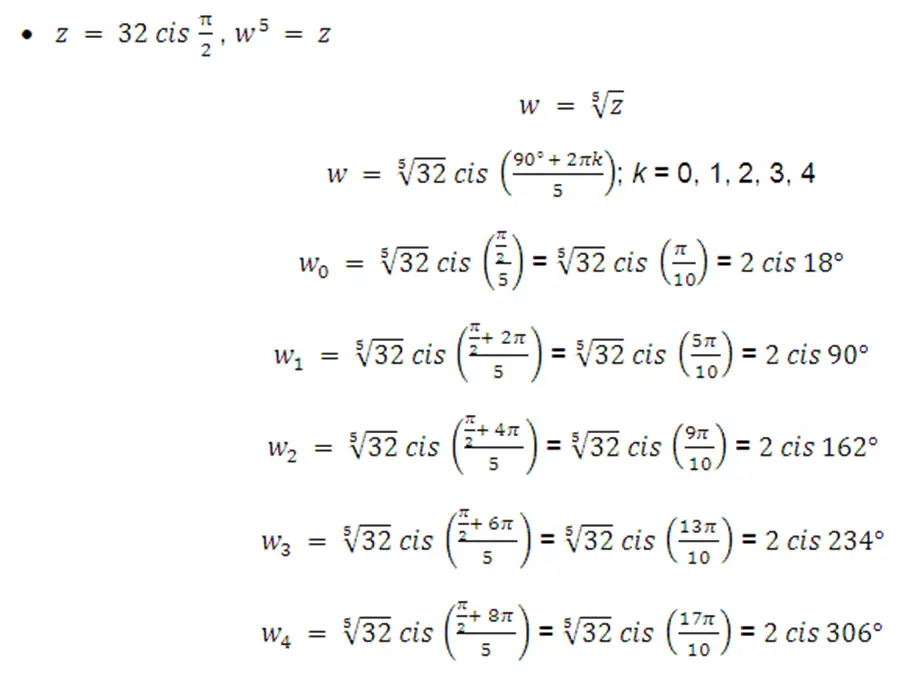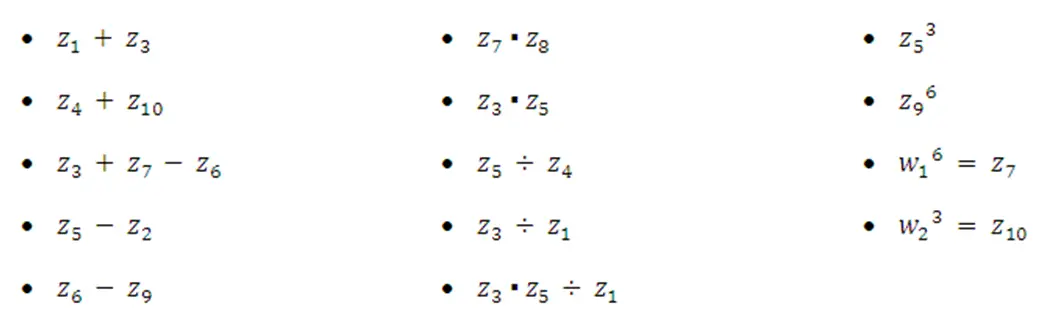50 Ejemplos De Operaciones Con Números Complejos
Las operaciones con números complejos, son el elemento necesario para completar la constitución de este conjunto numérico en un cuerpo algebraico.
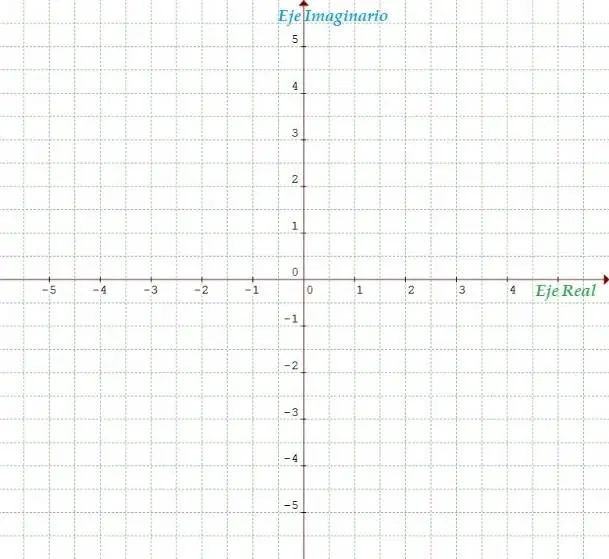
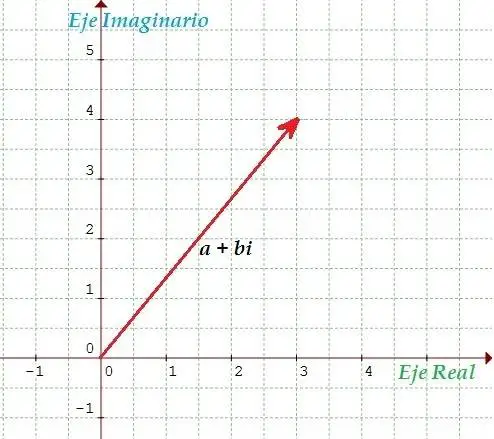
La construcción axiomática del conjunto de los números complejos se fue desarrollando con el avance de la matemática, la física y posteriormente la electrónica y se concretó después de tres siglos al ser representados por puntos o vectores en el plano numérico de Gauss.
fig. 1 Plano numérico de Gauss
Operaciones con números complejos como un par de la forma (a; b)
Propiedades de la adición
Asociativa
La adición es una operación entre dos elementos para obtener su suma, si se tienen más de dos elementos uno los puede agrupar de cualquier manera seleccionando primero dos de ellos y al resultado se le suma otro elemento y así hasta culminar los elementos que se querían sumar.
Conmutativa
El orden en que se suman dos elementos es indistinto y se obtendrán siempre los mismos resultados.
Neutro
Multiplicación
Propiedades de la multiplicación
Asociativa
La multiplicación es una operación entre dos elementos para obtener su producto, si se tienen más de dos elementos uno los puede agrupar de cualquier manera seleccionando primero dos de ellos y al resultado se le multiplica otro elemento y así hasta culminar los elementos que se querían multiplicar.
Conmutativa
El orden en que se multiplican dos elementos es indistinto y se obtendrán siempre los mismos resultados. De ahí el dicho de que “El orden de los factores no altera el producto”
Ejemplos:
División
Consideremos el par (a; 0) correspondiente al número real a. Pues bien con él podremos realizar sin ningún problema las operaciones de adición
(a; 0) + (b; 0) = a + b
(a; 0) + (b; 0) = (a + b; 0)
donde a + b ∈ R
Igual para la multiplicación y la división.
(a; 0) ▪ (b; 0) = a ▪ b
(a; 0) ▪ (b; 0) = (a ▪ b; 0)
(a; 0) ÷ (b; 0) = a/b
(a; 0) ÷ (b; 0) = (a/b; o)
donde (a/b) ∈ R
Visto así se puede establecer una correspondencia biunívoca entre el conjunto de pares de la forma (a; 0) y el conjunto de los números reales.
Tomemos ahora el par (0; 1) y con la operación de multiplicación definida tenemos:
(0; 1) ▪ (0; 1) = (0 – 1; 0 + 0) = (- 1; 0)
Si definimos la unidad imaginaria i = (0; 1), tenemos que:
i ▪ i = – 1
Por tanto, el número complejo de la forma (a; b) lo podemos escribir:
(a; b) = (a; 0) + (b; 0) ▪ (0; 1) = a + b ▪ i
Operaciones con números complejos como un vector de la forma z = a + bi
fig. 2 numero complejo de la forma a + bi
Adición
Sea a, b, c y d ∈ R
(a + bi) + (c + di) = (a + c) + (b + d)i
Ejemplos:
Propiedades de la adición
Asociativa
Propiedades de la multiplicación
Asociativa:
Solo nos falta definir la potenciación y radicación de los números complejos, para ello trabajaremos la representación geométrica de los mismos.
Operaciones co números complejos en forma trigonométrica z = r cis a
fig. 3 numero complejo de la forma r cis a
Multiplicación
División
Ejemplos:
Potenciación
Como la multiplicación de números complejos es asociativa podemos introducir la noción de potencia de un número complejo.
Definamos w como el resultado de multiplicar n veces el número complejo z.
w = z ▪ z ▪ z ▪ z ▪…▪ z
n veces
w es la n-ésima potencia del número complejo z
w = z^n
Si , usando la fórmula de Moivre, tenemos que:
z^n = r^n (cosnα + i sinnα )
Potencias de i
Cada vez que aumenta el exponente de i, cuatro unidades se repite el valor de la potencia
Radicación
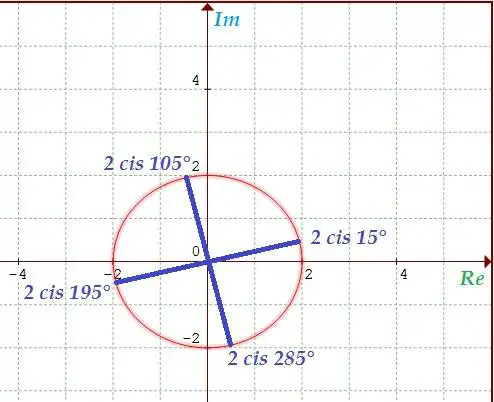
fig. 4 raíz cuarta de 16 cis 60°
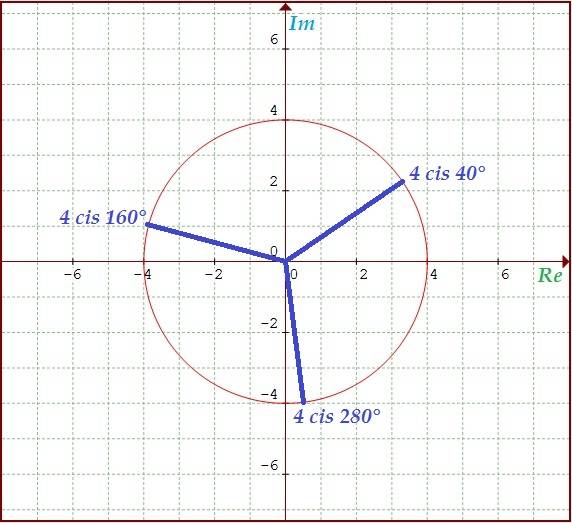
fig. 5 raíz tercera de 64 cis 120°
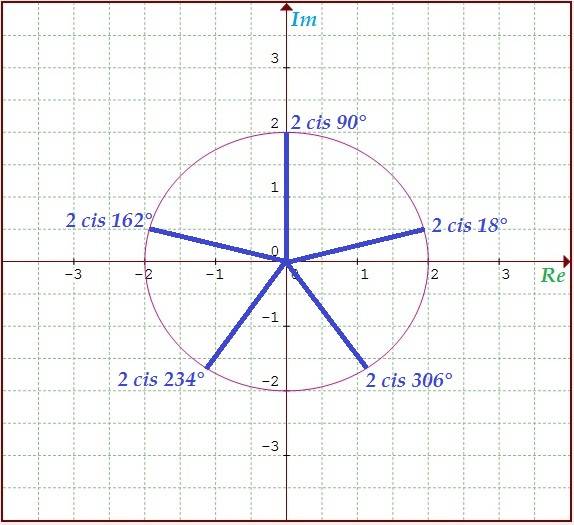
fig. 6 raíz tercera de 32 cis 90°
Ejercicios:
Hallar
Con las operaciones con números complejos completamos los ejemplos de todos los conjuntos numéricos Naturales (N), Enteros (Z), Racionales (Q), Reales (R) y Complejos (C),
[sc name=»educacion»]Ángel Míguez Álvarez