Ejemplos de Conjuntos
Un conjunto es una colección o grupo de objetos, números o elementos que comparten una o varias características en común. Los elementos de un conjunto pueden ser cualquier cosa, desde números y letras hasta objetos físicos o conceptuales.
Los conjuntos se representan con llaves {} y se separan los elementos por comas.
- Por ejemplo, el conjunto de los números pares menores que 10 se puede escribir como {2, 4, 6, 8}. En este caso, los elementos son números y la característica común es que todos son pares y menores que 10.
Los conjuntos pueden ser finitos o infinitos, según la cantidad de elementos que contienen. Además, pueden ser disjuntos (sin elementos en común) o superpuestos (con elementos en común). También pueden ser equivalentes, si tienen los mismos elementos, o subconjuntos, si todos los elementos de un conjunto están contenidos en otro conjunto.
Ejemplos de Conjuntos:
| Cinco libros | Diez lápices de colores | Dos maestras | Ocho sillas |
| Cuatro cuadernos | Dos ventanas | Seis estudiantes | Tres cuentos |
| Una cartelera | Una Puerta | Cinco galletas | Dos sombreros |
Formas de expresar un conjunto
Los Conjuntos se pueden expresar de dos maneras:
Por extensión: cuando mencionamos sus elementos uno por uno.
- Por ejemplo, el conjunto de los días de la semana: Lunes, martes, miércoles, jueves, viernes, sábado, domingo.
- Otro ejemplo serían las estaciones del año: Primavera, verano, otoño, invierno.
- Un ejemplo con nombres femeninos sería: Margarita, Jéssica, Gisela.
Por comprensión: cuando mencionamos la característica común de sus elementos. Si utilizamosm como referencia los 3 ejemplos anteriores podríamos expresarlos tambien de la siguiente manera:
- Días de la semana
- Estaciones del año
- Nombres femeninos
Notación de conjuntos
Regularmente en Matemáticas se representan los conjuntos con letras mayúsculas y los elementos con letras minúsculas.
- Por ejemplo, el conjunto A cuyos elementos son a, b, c, d, e los expresamos de manera escrita así: A= {a, b, c, d, e}
Se usan también pictogramas para representar algunos conjuntos por extensión.
- Por ejemplo, el conjunto B de los juguetes de Jaimito
Se usan también palabras que distinguen los elementos que se agrupan en un conjunto.
- un ejemplo de este caso sería este conjunto C de las cualidades de Federico: C= {bondadoso, parlanchín, gracioso, juguetón}
- Este conjunto D de los primeros cinco números impares: D = {1, 3, 5, 7, 9}
- El conjunto E de los números primos de una sola cifra: E = {1, 2, 3, 5, 7}
- El conjunto F de los números naturales pares menores que 20: F = {2, 4, 6, 8, 10, 12, 14, 16, 18}
- El conjunto G de los múltiplos de tres: G = {Todos los números de la forma 3 . x ∈ N}
Conjuntos infinitos
Los conjuntos infinitos se pueden denotar de dos maneras:
Por comprensión:
- Ejemplo: El conjunto H de los números naturales: H = N
Por extensión, colocando puntos suspensivos para indicar que no existe un último elemento de este conjunto:
- Ejemplo: El conjunto H de los números naturales: H = {1, 2, 3, 4, 5, 6, 7 , 8, 9, 10, 11, 12…}
Símbolos usados en la Teoría de Conjuntos
| Símbolo | Como se lee |
| a ∈ R | El elemento a pertenece al conjunto |
| b ∈ Z | El elemento b no pertenece al conjunto |
| c ⊂ D | El elemento c está contenido en el conjunto D |
| {x, y} ⊂ D | Los elementos x, y están contenidos en el conjunto D |
| e ⊄ F | El elemento e no está contenido en el conjunto F |
| {z, w} ⊄ F | Los elementos z, w no están contenidos en el conjunto F |
| G ⊂ H | El conjunto G es subconjunto del conjunto H |
| I ⊄ J | El conjunto I no es subconjunto del conjunto J |
| Ø | Conjunto vacío, no tiene elementos |
Subconjuntos
Si tenemos dos conjuntos, A y B, si todos los elementos del conjunto A pertenecen al conjunto B, entonces podemos señalar que el conjunto A es un subconjunto del conjunto B.
- Ejemplo: Sea A el conjunto de todos los estudiantes de la escuela de mi pueblo y sea B el conjunto de todas y todos los estudiantes de segundo curso
B ⊂ A
- Ejemplo: Sea el conjunto de los números naturales y sea el conjunto de todos los números pares
P ⊂ N
Diagramas de Venn
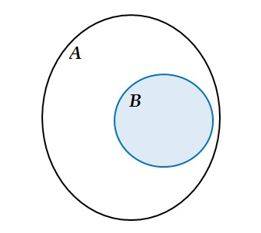
Son unos gráficos que se utilizan para hacer objetivo un conjunto o un subconjunto o relaciones entre conjuntos. Ayudan a poner en evidencia ciertos conceptos, aunque no constituyen una definición, ni demostración.
- Ejemplo: B es subconjunto de A
fig. 1 Diagrama de Venn
Conjuntos Iguales
Dos conjuntos son iguales si tienen los mismos elementos.
- Ejemplo: Sea A = {1, 3, 5, 7, 9} y sea B = {3, 7, 9, 1, 5} entonces A = B
- Otro ejemplo: Sea C = los números pares de una sola cifra y sea D = {2, 4, 6, 8}, entonces C = D
Conjuntos Diferentes
Dos conjuntos son diferentes si no tienen los mismos elementos.
- Por Ejemplo: Sea E = {1, 3, 5, 7, 9} y sea F = {1, 3, 5, 7} entonces E ≠ F
- Otro ejemplo: Sea G = los números pares y sea H = {0, 1, 2, 3} entonces G ≠ H