Ejemplos De Ecuaciones De Segundo Grado
Las ecuaciones de segundo grado son ecuaciones algebraicas que tienen una variable elevada al cuadrado (x2) y pueden ser escritas en la forma ax2 + bx + c = 0, donde a, b, y c son coeficientes numéricos.
- Por ejemplo, la ecuación x2 + 5x + 6 = 0 es una ecuación de segundo grado. Para resolver esta ecuación, podemos seguir los siguientes pasos:
1. Identificar los coeficientes a, b y c de la ecuación. En este caso, a = 1, b = 5 y c = 6.
2. Utilizar la fórmula general para ecuaciones de segundo grado:
x = (-b ± √(b2 – 4ac)) / 2a
3. Sustituir los valores de a, b y c en la fórmula y resolver para x:
x = (-5 ± √(52 – 4(1)(6))) / 2(1)
x = (-5 ± √1) / 2
x1 = -3
x2 = -2
Por lo tanto, las soluciones para la ecuación x2 + 5x + 6 = 0 son x1 = -3 y x2 =-2.
Es importante recordar que las ecuaciones de segundo grado son importantes en la matemática y en la física, ya que se utilizan para modelar situaciones en las que una cantidad varía de forma cuadrática. Por ejemplo, la distancia recorrida por un objeto en caída libre puede ser modelada por una ecuación de segundo grado.
También es importante tener en cuenta que las ecuaciones de segundo grado pueden tener dos soluciones distintas, una solución doble o ninguna solución, dependiendo de los valores de los coeficientes. Además, algunas veces las soluciones pueden ser números complejos, lo que significa que involucran la raíz cuadrada de números negativos.
Explicación sencilla
Las ecuaciones de segundo grado son aquellas donde la incógnita esté por lo menos una vez elevada al cuadrado (x2) y que puedan expresarse de la siguiente forma: ax2 + bx + c = 0 donde:
- a es el coeficiente de x2. No puede ser cero (0).
- b es el coeficiente de x (el término de primer orden)
- c es el término independiente.
- Un ejemplo de ecuación de segundo grado es: – x2 – 5x + 6 = 0. Otro ejemplo es – 4x2 – 12x + 1 = 0.
Ejemplos de ecuaciones de segundo grado
| x2 – 5x + 6 = 0 | 2x2 – 7x + 3 = 0 | x2 + 3x – 4 = 0 |
| x2 – 9 = 0 | 2x2 – 10x + 12 = 0 | 3x2 – 8x – 3 = 0 |
| x2 – 4x – 5 = 0 | 4x2 + 7x- 3 = 0 | x2 – 2x + 1 = 0 |
| x2 – 6x + 8 = 0 | 3x2 + 5x – 2 =0 | 2x2 – 3x – 2 = 0 |
| x2 + 2x – 3 = 0 | 5x2 – 7x – 2 = 0 | x2 + 4x + 3 = 0 |
| 3x2 – 2x – 5 = 0 | x2 – 3x – 10 = 0 | 2x2 – 11x + 12 = 0 |
| x2 + 6x + 9 = 0 | 4x2 – 12x + 9 = 0 | 3x2 – 4x – 3 = 0 |
| x2 – 8x + 15 = 0 | x2 + x – 6 = 0 | 2x2 + 5x – 3 = 0 |
| x2 + 7x + 10 = 0 | 5x2 – 11x + 6 = 0 | x2 – 2 = 0 |
| 2x2 – 8x + 6 = 0 | x2 + 5x + 6 = 0 | 3x2 – 10x + 7 = 0 |
| x2 – 5x + 6 = 0 | 4x2 – 4x – 3 = 0 | x2 – 7x + 10 = 0 |
| 2x2 + 3x – 2 = 0 | x2 – 2 = 0 | 3x2 + 4x – 2 = 0 |
| 2x2 – 5x + 2 = 0 | x2 – 10x + 25 = 0 | 4x2 + 4x+ 1 = 0 |
| x2 – 4x + 4 = 0 |
Resolución de ecuaciones de segundo grado
Las soluciones de una ecuación de segundo grado se calculan usando la fórmula cuadrática:
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
Donde a, b y c son los coeficientes de la ecuación.
- Ejemplo: Resuelve la ecuación: 2x2 + 3x – 5 = 0
Paso 1: Identifica los coeficientes a, b y c en la ecuación general ax2 + bx + c = 0.
En este caso, a = 2, b = 3 y c = -5.
Paso 2: Sustituye los valores de a, b y c en la fórmula general:
x = [-b ± √(b2 – 4ac)] / 2a
x = [-3 ± √(32 – 4(2)(-5))] / 2(2)
Paso 3: Resuelve la ecuación y simplifica.
x = [-3 ± √(9 + 40)] / 4
x = [-3 ± √49] / 4
x = (-3 + 7) / 4 o x = (-3 – 7) / 4
Paso 4: Simplifica la solución.
x = 1/2 o x = -5/2
Por lo tanto, las soluciones de la ecuación 2x2 + 3x – 5 = 0 son x = 1/2 y x = -5/2.
Algo muy importante a destacar es que siempre existe dos soluciones para una ecuación de segundo grado, llamadas raíces o soluciones. Estas dos raíces suman el coeficiente lineal b y multiplicadas dan el término independiente c.
Representación gráfica de ecuaciones de segundo grado
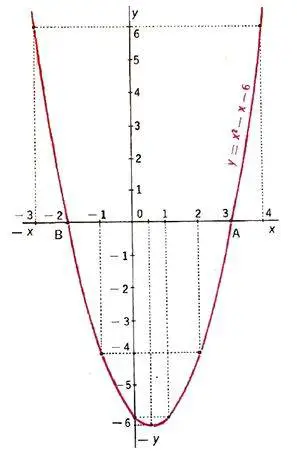
Usando como ejemplo la ecuación de segundo grado x2 – x – 6 = 0, se dan valores a la variable independiente x y usando la función calcularemos para que la variable dependiente y tome sus valores.
$$\begin{array}{cc}x&y\\0&-6\\1/2&-6,25\\1&-6\\2&-4\\3&0\\4&6\\-1&-4\\-2&0\\-3&6\end{array}$$
Y utilizando estos pares en el plano cartesiano podemos hacer la representación gráfica:
Ecuaciones de segundo grado y su uso en la vida cotidiana
Las ecuaciones de segundo grado se utilizan en muchos aspectos de la vida cotidiana, desde la ingeniería y la física hasta la economía y las finanzas.
- En el diseño de puentes los ingenieros usan las ecuaciones de segundo grado para calcular la forma y la resistencia de los arcos y vigas que se utilizan en la construcción de puentes.
- Las ecuaciones de segundo grado se utilizan en la física para calcular la trayectoria de un objeto en movimiento, como un proyectil que se dispara desde un cañón.
- Tambien se utilizan en la economía para modelar la oferta y la demanda de bienes y servicios en un mercado.
- En las finanzas se utilizan para calcular el costo de los préstamos y los intereses, así como para modelar el crecimiento de las inversiones.
- Las ecuaciones de segundo grado se utilizan en la medicina para modelar la propagación de enfermedades infecciosas y para calcular la dosis correcta de medicamentos.
- Se utilizan en la informática para modelar procesos de aprendizaje automático y para calcular la complejidad de los algoritmos.