25 Ejemplos de líneas y puntos notables de un Triangulo
Un triángulo es una figura geométrica que se forma con tres segmentos de recta que cumpla con la condición de que la suma de dos cualesquiera de ellas es mayor que el tercero, llamada la desigualdad triangular.
Ejemplos:
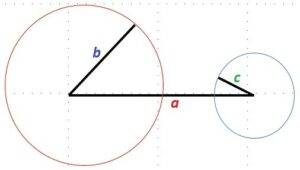
- Dados los segmentos:
Fig. 1 segmentos desiguales a > b > c
Fig. 2 no cumple desigualdad triangular b + c < a
Por tanto, pese a tener tres segmentos, no podemos formar con ellos un triángulo.
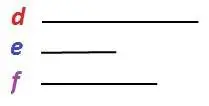
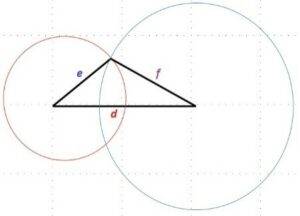
- Dados los segmentos:
Fig. 3 segmentos desiguales d > f > e
Fig. 4 si cumple desigualdad triangular d + e > f, d + f > e, f + e > d
Por tanto, al cumplir con la desigualdad triangular, estos tres segmentos, pueden formar un triángulo.
Rectas Notables de un triángulo
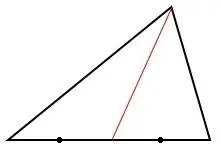
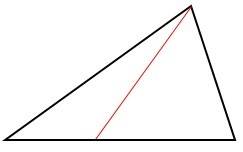
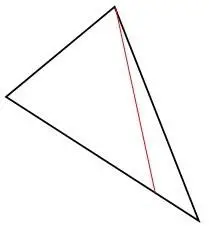
La ceviana
La ceviana en un triángulo, es cualquier segmento de recta que une uno de sus vértices con un punto en el lado opuesto o en una prolongación del lado opuesto.
Ejemplos:
 |
 |
 |
|
Fig. 5 ceviana interior |
Fig. 6 ceviana interior |
Fig. 7 ceviana exterior |
La mediana
Es una ceviana que une el vértice de un triángulo con el punto medio del lado opuesto. Las medianas de un triángulo cortan al triángulo en dos triángulos de igual área.
Ejemplo:
Fig. 8 mediana
La bisectriz
Es una ceviana que biseca o divide en dos ángulos iguales el ángulo de un vértice del triángulo.
Ejemplo:
Fig. 9 bisectriz
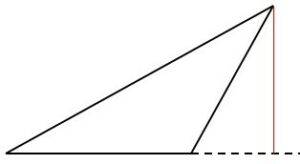
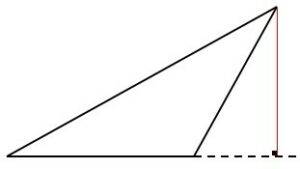
La altura
Es una ceviana perpendicular al lado opuesto al vértice del triángulo, puede ser interior o exterior al triángulo.
Ejemplos:
 |
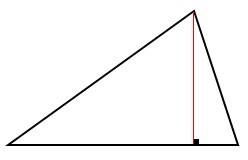 |
|
Fig. 10 altura exterior |
Fig. 11 altura interior |
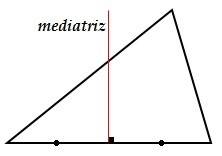
La mediatriz
Es una recta que pasa por el punto medio de un lado del triángulo y es perpendicular a ella.
Ejemplo:
Fig. 12 mediatriz
Puntos Notables de un triángulo
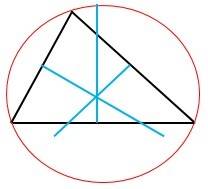
El circuncentro
Es el punto donde se encuentran las tres mediatrices de un triángulo.
Ejemplo:
Fig. 13 circuncentro
Este punto de intersección de las mediatrices se denomina circuncentro ya que equidista de los tres vértices del triángulo y sirve de centro de la circunferencia circunscrita a dicho triángulo.
Ejemplo:
Fig. 14 circunferencia circunscrita
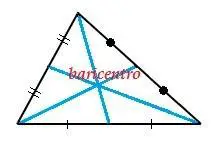
El baricentro
Es el punto donde se encuentran las tres medianas de un triángulo.
Ejemplo:
Fig. 15 baricentro
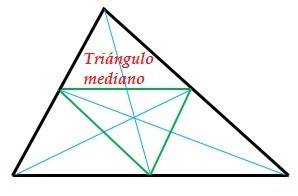
El baricentro corta a todas las medianas en una relación 2:1. Si trazamos un segmento que una los puntos medios de cada lado del triángulo se forma el triángulo mediano que divide al triángulo original en cuatro triángulos de igual área.
Ejemplo:
Fig. 16 triángulo mediano
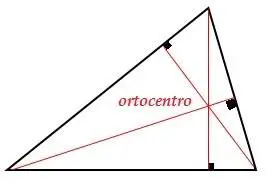
El ortocentro
Es el punto donde se cortan las tres alturas de un triángulo.
Ejemplo:
Fig. 17 ortocentro
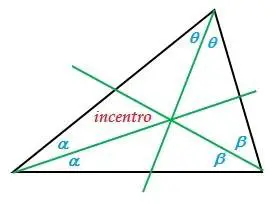
El incentro
Es el punto donde se cortan las tres bisectrices de los vértices del triángulo.
Ejemplo:
Fig. 18 incentro
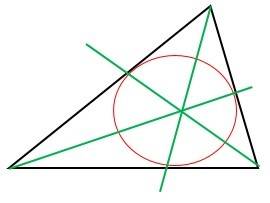
El incentro equidista de los lados del triángulo, por lo que se puede trazar una circunferencia interior al triángulo, una circunferencia inscrita, con centro en este punto y resultará tangente a los tres lados del triángulo.
Este punto también es considerado el centro de gravedad del triángulo.
Ejemplo:
Fig. 19 circunferencia inscrita
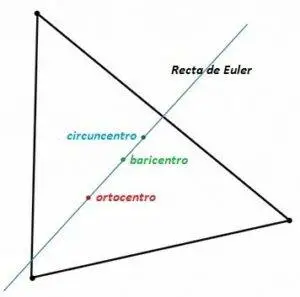
La recta de Euler
La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo cualquiera.
Esto demuestra que la posición de estos tres puntos notables del triángulo son colineales.
En 1 765 se realizó este descubrimiento, el cual se le debe al matemático suizo Leonard Euler.
Adicionalmente, como curiosidad, se estableció que la distancia del baricentro al circuncentro es la mitad de la distancia del baricentro al ortocentro.
Ejemplo:
Fig. 20 Recta de Euler
Ejercicios
- Sea el triángulo definido por los siguientes vértices: A (2, 2); B (-2, 0); C (2, 4). Calcular las longitudes de las tres medianas.
- Sea el triángulo definido por los siguientes vértices: A (5, 1); B (-2, 4); C (-1, -2). Calcular la ecuación las tres medianas.
- Tomemos un triángulo que está definido por los siguientes vértices: A (3, 6); B (5, 2); C (1, -2). Calcular las ecuaciones de las tres alturas y determinar el ortocentro del triángulo.
- Sea el triángulo que está definido por los siguientes vértices: A (1, -2); B (13, 3); C (1, 9). Calcular su circuncentro.
- Tomemos un triángulo que tiene los siguientes vértices: A (2, 2); B (9, 7); C (11, -3). Calcular:
-
- El baricentro.
- El circuncentro.
- El ortocentro.
-
- Sea el triángulo de vértices: A (-1, -1); B (7, 5); C (2, 7). Calcular:
-
- El baricentro.
- Las ecuaciones de las tres alturas.
- El ortocentro.
- La recta de Euler.
-