Ejemplos de Cómo calcular el área de un polígono irregular
El área de un polígono irregular se puede calcular dividiéndolo en formas más simples, como triángulos o rectángulos, y luego sumando las áreas de cada forma. Este método se llama descomposición en formas más simples.
- Por ejemplo, si tenemos un polígono irregular con forma de «L», podemos dividirlo en un triángulo y un rectángulo. Para calcular el área del polígono, primero calculamos el área del triángulo utilizando la fórmula para el área de un triángulo:
Área del triángulo = base x altura / 2
En este caso, la base del triángulo es 4 unidades y la altura es 3 unidades:
Área del triángulo = 4 x 3 / 2 = 6 unidades cuadradas
Luego, calculamos el área del rectángulo multiplicando su base por su altura:
Área del rectángulo = base x altura
Área del rectángulo = 3 x 2 = 6 unidades cuadradas
Finalmente, sumamos las áreas del triángulo y del rectángulo para obtener el área total del polígono:
Área total del polígono = Área del triángulo + Área del rectángulo
Área total del polígono = 6 + 6 = 12 unidades cuadradas
Por lo tanto, el área del polígono es de 12 unidades cuadradas.
La descomposición en formas más simples puede ser más difícil de hacer en polígonos irregulares más complejos. Además, se deben tener en cuenta las unidades de medida al calcular el área, y es importante verificar que todas las medidas estén en la misma unidad antes de realizar los cálculos.
Explicación sencilla
Calcular el área de un polígono irregular puede parecer desafiante, pero con algunos conceptos básicos y las herramientas adecuadas, se convierte en un proceso sencillo y accesible para cualquier persona.
En primer lugar, es importante entender que un polígono irregular es aquel que no se puede clasificar como un polígono regular, es decir, que sus lados no tienen la misma longitud ni sus ángulos la misma medida. Por lo tanto, no podemos aplicar una fórmula general para calcular su área como lo haríamos con un polígono regular.
Sin embargo, podemos descomponer el polígono irregular en figuras más simples, como triángulos, cuadriláteros o trapecios, cuyas áreas podemos calcular con fórmulas bien conocidas. Luego, podemos sumar las áreas de estas figuras para obtener el área total del polígono irregular. Luego, podemos calcular el área de cada figura por separado.
Para obtener una buena aproximación del área real del polígono irregular, es necesario que las figuras en las que se descompone sean lo más simples posible y que las mediciones de los lados y ángulos sean lo más precisas posible. Además, es fundamental tener una comprensión sólida de las fórmulas de área de las figuras simples y saber cómo aplicarlas correctamente.
Ejemplos de cómo calcular el área de un polígono irregular
| Método de triangulación: Dividir el polígono en triángulos, calcular el área de cada uno de ellos y sumarlos para obtener el área total del polígono. |
| Método de las coordenadas: Si conocemos las coordenadas de los vértices del polígono, podemos utilizar la fórmula de Shoelace para calcular el área. |
| Método de la red: Dibujar una red cuadriculada sobre el polígono, contar los cuadrados que quedan completamente dentro del polígono y multiplicar por el área de cada cuadrado. |
| Método de las figuras de referencia: Dibujar figuras de referencia, como rectángulos o triángulos, que contengan al polígono y restar las áreas de las partes que quedan fuera del polígono. |
| Método de Monte Carlo: Generar un gran número de puntos aleatorios dentro de un rectángulo que contenga al polígono, contar cuántos de estos puntos caen dentro del polígono y utilizar esta proporción para estimar el área. |
| Método del círculo: Dibujar un círculo grande que contenga al polígono, calcular suárea y luego restar las áreas de las partes del círculo que quedan fuera del polígono. |
| Método de la integración: Si conocemos una ecuación que describa la forma del polígono, podemos utilizar técnicas de cálculo integral para encontrar su área. |
| Método del polígono convexo: Si el polígono es convexo, podemos utilizar la fórmula de la apotema y la longitud de los lados para calcular el área. |
| Método de la aproximación por rectángulos: Dividir el polígono en pequeños rectángulos, calcular el área de cada uno y sumarlos para obtener una aproximación del área total. |
| Método de la aproximación por curvas: Dividir el polígono en pequeñas curvas, calcular el área de cada una y sumarlas para obtener una aproximación del área total. Este método es más preciso que el anterior en polígonos irregulares con curvas suaves. |
Paso a paso de cómo calcular el área de un polígono irregular
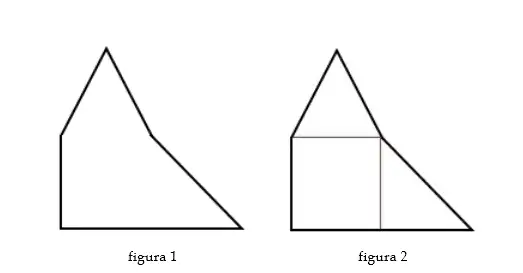
Tomando como ejemplo el polígono irregular de la figura 1, se puede dividir en tres polígonos regulares conocidos como se muestra en la figura 2: un triángulo equilátero, un cuadrado y un triángulo rectángulo.
En este caso en específico se calcularían las áreas de estas tres figuras por separado, se sumarían y esta suma nos daría como resultado el área del polígono irregular.
¿Qué es un polígono?
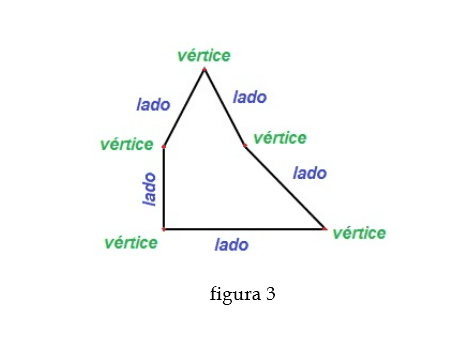
Un polígono es una figura en el plano, conformado por segmentos de rectas que llamaremos lado del polígono y estos se unen a otros segmentos en un punto que llamaremos vértice.
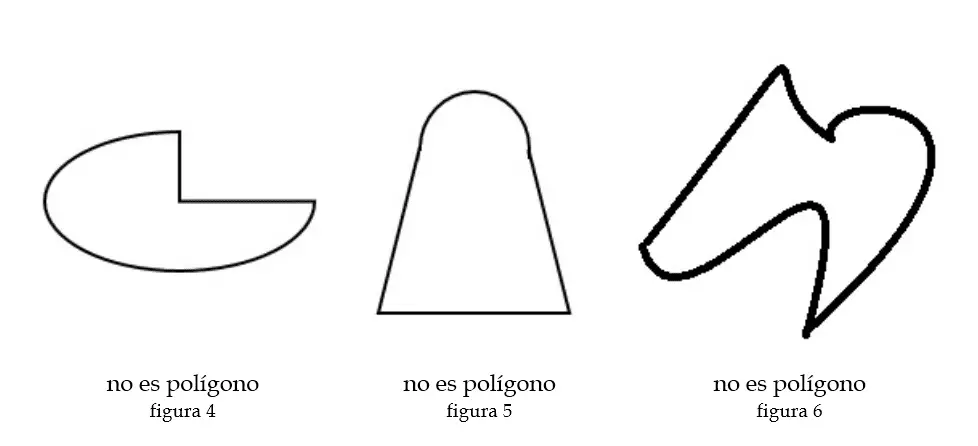
Cualquier otra figura cuyos componentes no sean segmentos de recta, no es un polígono.
Tipos de Polígonos
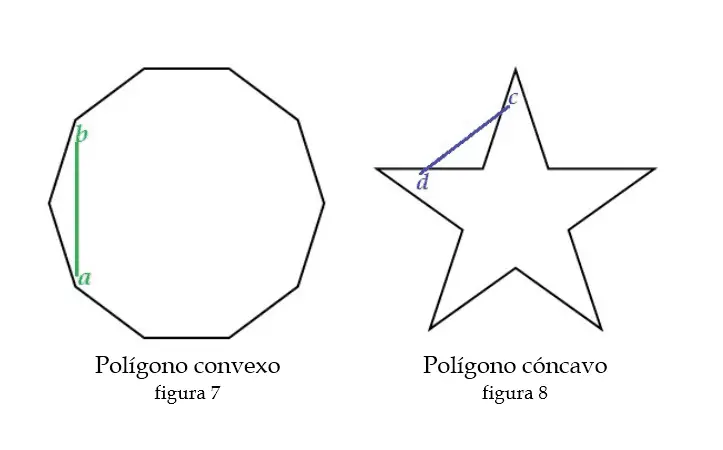
Un Polígono es convexo cuando tomamos un par de puntos cualesquiera a y b pertenecientes a él y al trazar un segmento de recta que los une, el segmento queda en su totalidad dentro del Polígono.
Un Polígono es cóncavo cuando existen, por lo menos, un par de puntos c y d pertenecientes a él y al trazar un segmento de recta que los une, el segmento no queda totalmente en el interior del Polígono.
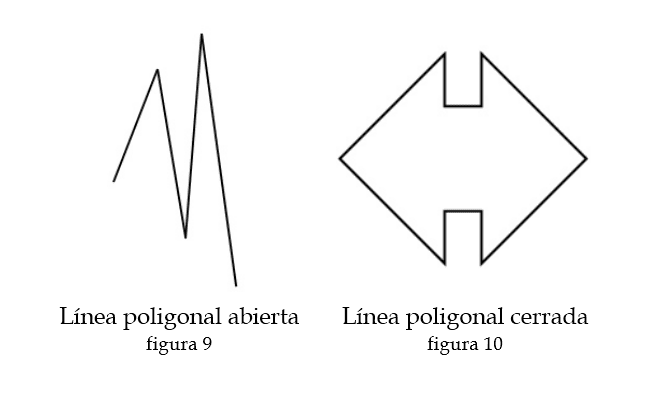
Líneas poligonales
Las líneas poligonales, como su nombre lo indica, son segmentos de rectas unidos por un vértice y pueden ser de dos tipos, abiertas o cerradas.
Las líneas poligonales cerradas se convierten en polígonos.
Las áreas de los Polígonos irregulares han sido usadas históricamente para delimitar las tierras de cultivo en terrenos de topografías irregulares, atravesados por ríos, desniveles o cadenas montañosas.