Ejemplos de cómo sacar el área de un Triángulo
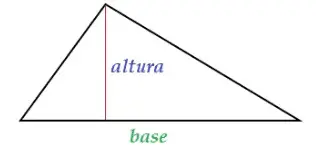
El área de un triángulo es la cantidad de espacio que ocupa su superficie. Para calcular el área de un triángulo, necesitamos conocer su base y su altura.
La fórmula para calcular el área de un triángulo es:
Área = (base x altura) / 2
- Por ejemplo, si tenemos un triángulo con una base de 6 centímetros y una altura de 4 centímetros, podemos calcular su área de la siguiente manera:
Área = (base x altura) / 2
Área = (6 cm x 4 cm) / 2
Área = 24 cm² / 2
Área = 12 cm²
Por lo tanto, el área del triángulo es de 12 centímetros cuadrados.
La base y la altura del triángulo deben estar en la misma unidad de medida. Además, la altura del triángulo debe ser perpendicular a la base para poder calcular el área correctamente.
Explicación sencilla
El área de un triángulo es una de las medidas más importantes en la geometría. Se define como la mitad del producto de su base y su altura. La base es cualquier lado del triángulo y la altura es la distancia perpendicular desde la base hasta el vértice opuesto.
- Por ejemplo, si tenemos un triángulo con una base de 6 unidades y una altura de 4 unidades, podemos calcular su área utilizando la fórmula del área del triángulo:
Área = 1/2 * base * altura
Área = 1/2 * 6 unidades * 4 unidades
Área = 12 unidades cuadradas
La base y la altura deben ser perpendiculares para poder utilizar esta fórmula. Si la altura no es perpendicular a la base, entonces se debe utilizar otra fórmula para calcular el área. La unidad de medida utilizada para la base y la altura debe ser la misma para que el resultado tenga sentido. Si la base está medida en metros, por ejemplo, la altura también debe estar medida en metros.
Ejemplos de cómo sacar el área de un triángulo
| Un triángulo con una base de 10 cm y una altura de 6 cm: Área = 1/2 * 10 cm * 6 cm = 30 cm2 |
| Un triángulo con una base de 7 m y una altura de 3 m: Área = 1/2 * 7 m * 3 m = 10.5 m2 |
| Un triángulo con una base de 5 in y una altura de 8 in: Área = 1/2 * 5 in * 8 in = 20 in2 |
| Un triángulo con una base de 12 ft y una altura de 9 ft: Área = 1/2 * 12 ft * 9 ft = 54 ft2 |
| Un triángulo con una base de 6 cm y una altura de 4 cm: Área = 1/2 * 6 cm * 4 cm = 12 cm2 |
| Un triángulo con una base de 15 m y una altura de 10 m: Área = 1/2 * 15 m * 10 m = 75 m2 |
| Un triángulo equilátero con un lado de 5 cm: Área = 1/2 * 5 cm * (5 cm/2) *sqrt(3) = 10.83 cm2 |
| Un triángulo isósceles con lados iguales de 6 in y una altura de 4 in: Área = 1/2 * 6 in * 4 in = 12 in2 |
| Un triángulo escaleno con lados de 7 cm, 9 cm y 12 cm, y una altura desde el lado de 9 cm de 8 cm: Área = 1/2 * 9 cm * 8 cm = 36 cm2 |
| Un triángulo rectángulo con una base de 10 ft y una altura de 8 ft: Área = 1/2 * 10 ft * 8 ft = 40 ft2 |
Ejemplos de métodos para sacar el área de un triángulo
Sacar el área de un triángulo conociendo su base y altura
Si b = 8 y h = 3, entonces el área del triángulo es igual a 12
Sacar el área de un triángulo conociendo su perímetro
Perímetro = a +b +c
Semi perímetro, s = (a + b + c)/2
Se utiliza la siguiente Fórmula de Herón para sacar el área del triángulo:
$$\sqrt{s(s-a)(s-b)(s-c)}$$
Si a=10, b=7, c=5 entonces s=11 y el área quedaría
$$\sqrt{11(11-10)(11-7)(11-5)}$$
$$\sqrt{11(1)(4)(6)}$$
$$\sqrt{264=}16,24807680947192…$$
¿Cómo calcular el área de un Triángulo geométricamente?
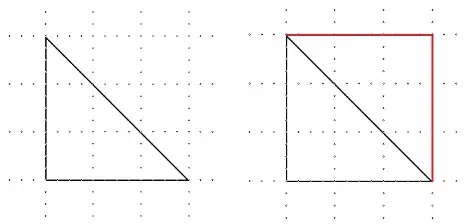
- Comparando la figura del triángulo con una figura conocida.
El área del cuadrado es l2. Si l = 3, entonces el área del triángulo = 4,5
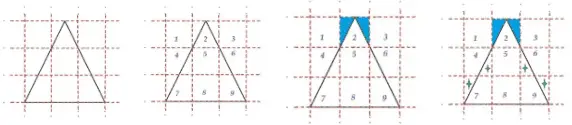
- Aproximando, cuadro a cuadro.
Describiendo el proceso tal cual se muestra en las cuatro figuras de la imagen superior:
- Hacemos una cuadrícula al triángulo
- Numeramos las cuadrículas
- El área azul equivale a la mitad de la cuadrícula
- Las áreas con la cruz verde son equivalentes
Una vez hechos estos pasos, si cada cuadrícula mide 1 cm2:
- Son 2 cm2 por las cuadrículas 5 y 8
- Es 0,5 cm2 en la cuadrícula 2
- Es 1 cm2 entre las cuadrículas 4 y 7
- Misma cantidad, 1cm2, con la 6 y 8