50 Ejemplos De Cómo Sacar Los Metros Cuadrados
Para sacar los metros cuadrados se requiere saber calcular el área de un polígono cualquiera, en dos y hasta en tres dimensiones.
Puede ser muy sencillo el cálculo del área que nos permite hallar los metros cuadrados de una superficie.
Pero puede ser tan complicado que necesitamos el auxilio de un topógrafo con el uso del teodolito y demás herramientas que le permitan decidir los metros cuadrados de un terreno cualquiera.
Ejemplos de cómo calcular los metros cuadrados
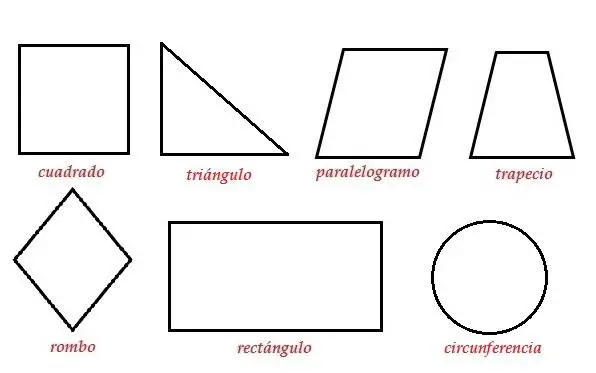
Caso ideal y más sencillo: Polígonos Regulares o Circunferencias
Se usa la fórmula de cálculo del área de la figura correspondiente y se obtienen los metros cuadrados que andamos buscando.
Cuadrado: lado al cuadrado.
Triángulo: base x altura entre dos.
Paralelogramo: base x altura.
Rectángulo: lado x lado.
Circunferencia: 2π x radio.
Rombo: diagonal menor x diagonal mayor.
Trapecio: la mitad de la suma de la base mayor más la base menor por la altura
Esto nos permitirá medir los metros cuadrados de un salón cualquiera, una mesa rectangular o redonda, una cancha deportiva, una pared a pintar y un largo etcétera.
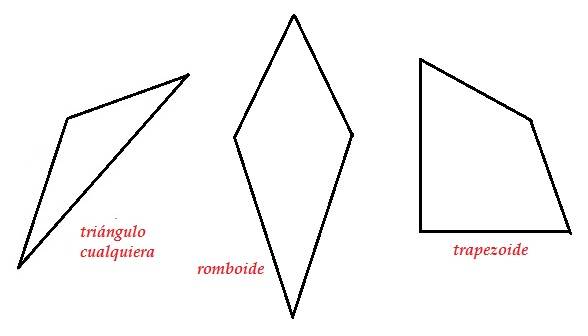
Caso sencillo: polígonos cualesquiera
Estos se pueden calcular fácilmente usando las fórmulas conocidas si subdividimos adecuadamente la figura.
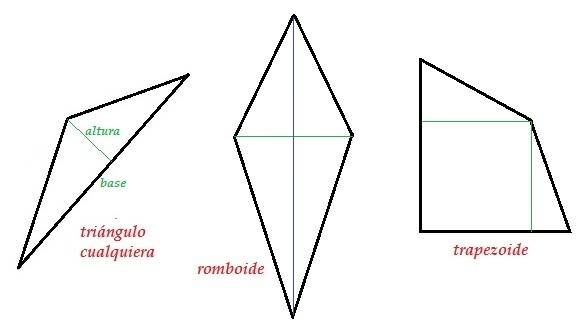
- Para un triángulo cualquiera se mide el lado que escogimos como base, medimos su altura y aplicamos la fórmula correspondiente. Puede ser una esquina exterior de un patio o terreno.
- En un romboide se puede dividir en dos o cuatro triángulos fáciles de calcular. Pude ser para calcular la superficie de una cometa y saber cuánto de papel de colores requiero en su construcción.
- Para un trapezoide se puede subdividir en triángulos y rectángulos. Por ejemplo, para establecer el espacio para la cancha de tenis y un área para gradas y otra para salones de servicio.
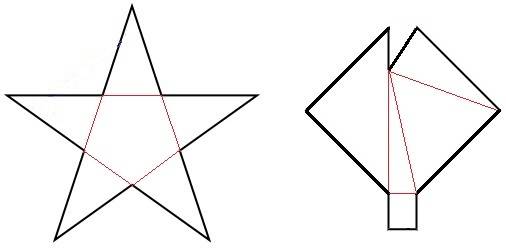
Caso metódico: Polígonos Irregulares Convexos y Cóncavos
Al igual que el caso anterior, estos se pueden calcular fácilmente usando las fórmulas conocidas si subdividimos adecuadamente la figura.
En el caso de la estrella, se convierte en cinco triángulos y un pentágono regular. Pudiera ser un diseño vanguardista de una sala de usos múltiples, que se puede convertir en cinco mini auditorios.
En el caso del fagocito, se convierte en cuatro triángulos y un rectángulo. Con base en la observación geométrica, todas estas figuras son convertibles y susceptibles de sacar sus metros cuadrados.
Caso mixto: Figuras no poligonales
La herramienta que se usa en los casos distintos a las figuras de formas conocidas es la subdivisión de las figuras irregulares o no poligonales a figuras conocidas. Veamos en este caso.
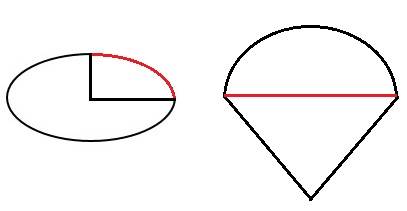
En el caso de la figura de la izquierda, Elipse, calculamos el área de la elipse (p x la mitad del eje mayor x la mitad del eje menor).
En el caso del campo de Béisbol, tenemos la mitad de una elipse y un triángulo.
Caso real en el campo: superficie irregular tridimensional
Para medir un terreno así, tienes dos posibilidades: curvas de nivel o triangulación de la superficie.
En cualquier caso se requieren de herramientas técnicas especializadas en este tipo de mediciones topográficas.
Tomada de: https://external-content.duckduckgo.com/iu/?u=https%3A%2F%2Ftse2.mm.bing.net%2Fth%3Fid%3DOIP.ZQoH8N1ndpJfygb1m55-UAHaEo%26pid%3DApi&f=1 y https://external-content.duckduckgo.com/iu/?u=https%3A%2F%2Ftse2.mm.bing.net%2Fth%3Fid%3DOIP.Y1DzM2TjoqbzXBCAKFuOtQAAAA%26pid%3DApi&f=1
Ejemplos con cálculos
Calcular el área del triángulo:
Calcular el área del trapezoide:
Calcular el área de la estrella:
Calcular el área de tres cuartos de elipse:
El cálculo de áreas es medular en la construcción, en el diseño de interiores, en la agricultura, en la planificación urbana y en un sinfín de áreas y especialidades profesionales.
Ángel Míguez Álvarez