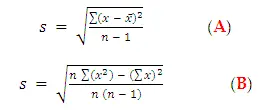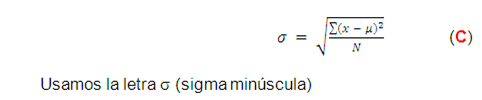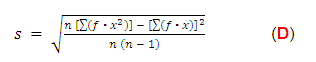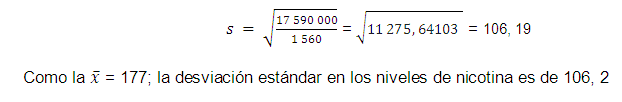15 Ejemplos De Medidas De Dispersión
Las medidas de dispersión son parámetros estadísticos que indican cuan dispersos están los valores de los datos estudiados respecto a sus medidas de tendencia central, sean muestrales o poblacionales, agrupados o no.
Se distinguen entre ellas el rango, la desviación estándar y la varianza. Las medidas de dispersión nos indican cuan alejados de la mitad o centro del conjunto de los datos estadísticos se distribuyen los mismos.
Estos parámetros estadísticos que trataremos acá son parte de la Estadística Descriptiva.
Ejemplos rápidos de medidas de dispersión
- La estatura de los estudiantes de 3er grado oscilaba entre 1, 21 y 1, 47 metros [Rango]
- La edad de las niñas del coro está entre 11 ± 2, 7 años [Desviación Estándar]
- Una vez ordenados los datos, 7, 29 es el valor de variación de los mismos. [Varianza]
Mediadas de Dispersión
Rango
Es la medida que nos indica la amplitud máxima de los datos en estudio.
Fórmula
Rango = (valor máximo) – (valor mínimo)
Ejemplo:
- Para los clientes del Banco SUR, el rango de variación de la espera para su atención en taquilla es 7 – 4 min = 3 min
Desviación Estándar
La desviación estándar es una medida de variación de todos los valores con respecto a la media.
- El valor de la desviación estándar s suele ser positivo. Sólo es igual a cero cuando todos los valores de los datos son el mismo número.
- Valores grandes de s indican mayores cantidades de variación o distancia respecto a la media aritmética.
- El valor de la desviación estándar s se puede aumentar con la inclusión de uno o más datos distantes (valores de datos que se encuentran muy distantes de los demás).
- Las unidades de la desviación estándar s (como segundos, metros, kilogramos, etc.) son las mismas de los datos originales.
Fórmulas
Desviación estándar (de un conjunto de valores muestrales): Es un tipo de desviación promedio de los valores, con respecto a la media, que se calcula utilizando las fórmulas:
Desviación estándar de una población
En la desviación estándar nos hemos referido hasta ahora a datos muestrales. Para calcular la desviación estándar de una población, se utiliza una fórmula ligeramente diferente: en lugar de dividir entre n – 1, se hace entre el tamaño N de la población, como en la siguiente expresión:
Desviación estándar con datos agrupados
donde x es la marca de clase de cada intervalo de los datos agrupados
Ejemplos:
- Atenea obtuvo las siguientes calificaciones en las cinco asignaturas que cursó en el cuarto semestre de su carrera: 3, 6, 5, 7 y 4
- Estudio realizado a 40 pacientes fumadores
Varianza de una muestra y una población
Usamos el término variación como una descripción general de la cantidad que varían los valores entre sí. (En ocasiones, se aplica el término dispersión en lugar de variación).
Varianza (de un conjunto de valores): medida de variación igual al cuadrado de la desviación estándar.
Formulas
Ejemplos:
- Sobre las calificaciones de Atenea (ejemplo anterior)
Si 1, 6 Þ VAR = 2, 1
Por tanto, la varianza respecto a la media es de 2, 1 puntos.
- En la evaluación de ingreso a una Universidad a 600 estudiantes les aplicaron un test de 80 preguntas.
Ejercicios de medidas de dispersión
- Se mide el índice de masa corporal de un grupo de vecinos de una cooperativa agrícola
| Edad | Estatura
(cm) |
Peso
(libras) |
Diámetro Cintura (cm) | Índice Masa Corporal |
| 17 | 164, 3 | 114, 8 | 67, 2 | 19, 6 |
| 32 | 166, 4 | 149, 3 | 82, 5 | 23, 8 |
| 25 | 162, 3 | 107, 8 | 66, 7 | 19, 6 |
| 55 | 162, 3 | 160, 1 | 93, 0 | 29, 1 |
| 27 | 159, 6 | 127, 1 | 82, 6 | 25, 2 |
| 29 | 163, 6 | 123, 1 | 75, 4 | 21, 4 |
| 25 | 159, 8 | 111, 7 | 73, 6 | 22, 0 |
| 12 | 163, 3 | 156, 3 | 81, 4 | 27, 5 |
| 41 | 167, 9 | 218, 8 | 99, 4 | 33, 5 |
| 32 | 161, 4 | 110, 2 | 67, 7 | 20, 6 |
| 31 | 166, 7 | 188, 3 | 100, 7 | 29, 9 |
| 19 | 164, 8 | 105, 4 | 72, 9 | 17, 7 |
| 19 | 163, 1 | 136, 1 | 85, 0 | 24, 0 |
| 23 | 166, 7 | 182, 4 | 85, 7 | 28, 9 |
| 40 | 166, 8 | 238, 4 | 126, 0 | 37, 7 |
| 23 | 164, 7 | 108, 8 | 74, 5 | 18, 3 |
| 27 | 165, 1 | 119, 0 | 74, 5 | 19, 8 |
| 45 | 161, 9 | 161, 9 | 94, 0 | 29, 8 |
| 41 | 164, 3 | 174, 1 | 92, 8 | 29, 7 |
| 56 | 163, 4 | 181, 2 | 105, 5 | 31, 7 |
| 22 | 160, 7 | 124, 3 | 75, 5 | 23, 8 |
| 57 | 163, 4 | 255, 9 | 126, 5 | 44, 9 |
| 24 | 162, 6 | 106, 7 | 70, 0 | 19, 2 |
| 37 | 160, 6 | 149, 9 | 98, 0 | 28, 7 |
| 59 | 163, 5 | 163, 1 | 104, 7 | 28, 5 |
| 40 | 158, 6 | 94, 3 | 67, 8 | 19, 3 |
| 45 | 160, 2 | 159, 7 | 99, 3 | 31, 0 |
| 52 | 167, 6 | 162, 8 | 91, 1 | 25, 1 |
| 31 | 163, 4 | 130, 0 | 74, 5 | 22, 8 |
| 32 | 164, 1 | 179, 9 | 95, 5 | 30, 9 |
| 23 | 162, 7 | 147, 8 | 79, 5 | 26, 5 |
| 23 | 161, 3 | 112, 9 | 69, 1 | 21, 2 |
| 47 | 158, 2 | 195, 6 | 105, 5 | 40, 6 |
| 36 | 163, 2 | 124, 2 | 78, 8 | 21, 9 |
| 34 | 160, 5 | 135, 0 | 85, 7 | 26, 0 |
| 37 | 165, 0 | 141, 4 | 92, 8 | 23, 5 |
| 18 | 161, 8 | 123, 9 | 72, 7 | 22, 8 |
| 29 | 168, 0 | 135, 5 | 75, 9 | 20, 7 |
| 48 | 167, 0 | 130, 4 | 68, 6 | 20, 5 |
| 16 | 157, 0 | 100, 7 | 68, 7 | 21, 9 |
Calcular su Rango, Desviación Típica y Varianza
- En un hospital infantil, para diagnosticar hidrocefalia, le miden a todos los recién nacidos la circunferencia de sus cabezas medidas en centímetros
Niños
40, 1 39, 8 42, 3 41, 0 42, 5 40, 9 35, 5 35, 7 41, 1 41, 4
42, 2 42, 3 43, 2 42, 2 42, 4 43, 2 39, 9 40, 9 40, 7 41, 7
41, 7 41, 0 40, 4 42, 0 41, 2 39, 7 41, 9 41, 3 40, 2 41, 0
41, 1 40, 4 39, 2 42, 8 41, 9 42, 8 41, 0 40, 9 42, 0 42, 6
41, 0 39, 6 40, 2 40, 9 40, 2 41, 8 41, 7 41, 7 40, 9 42, 8
Niñas
39, 3 40, 2 41, 3 38, 1 39, 6 40, 6 38, 6 40, 5 40, 5 40, 3
39, 5 40, 7 40, 2 38, 2 40, 3 42, 6 39, 9 40, 0 40, 7 38, 6
41, 0 43, 7 40, 0 40, 1 41, 0 40, 8 41, 0 40, 3 40, 2 39, 2
34, 4 41, 0 39, 6 40, 9 36, 9 43, 6 40, 2 40, 8 37, 8 41, 2
42, 0 38, 3 39, 6 38, 9 36, 3 39, 9 40, 3 40, 1 42, 0 41, 6
Calcular su Rango, Desviación Típica y Varianza
- Los meteorólogos estudian la cantidad de lluvia caída semanalmente durante 7 años en Damasco, medida en centímetros cúbicos
| Año 1 | Año 2 | Año 3 | Año 4 | Año 5 | Año 6 | Año 7 |
| 0 | 0 | 0 | 0, 04 | 0, 04 | 0 | 0, 05 |
| 0 | 0 | 0 | 0, 06 | 0, 03 | 0, 1 | 0 |
| 0 | 0 | 0 | 0, 71 | 0 | 0 | 0 |
| 0 | 0, 44 | 0, 14 | 0, 04 | 0, 04 | 0, 64 | 0 |
| 0, 05 | 0 | 0 | 0 | 0, 01 | 0, 05 | 0 |
| 0 | 0 | 0, 64 | 0 | 0 | 0 | 0 |
| 0, 01 | 0 | 0 | 0 | 0, 3 | 0, 05 | 0 |
| 0 | 0 | 0, 01 | 0 | 0 | 0 | 0 |
| 0 | 0, 01 | 0, 01 | 0, 16 | 0 | 0 | 0, 09 |
| 0, 12 | 0, 06 | 0, 18 | 0, 39 | 0 | 0, 1 | 0 |
| 0 | 0 | 0 | 0 | 0, 78 | 0, 49 | 0 |
| 0 | 0, 02 | 0 | 0 | 0, 01 | 0, 17 | 0 |
| 1, 41 | 0, 65 | 0, 31 | 0 | 0 | 0, 54 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0, 4 | 0, 28 |
| 0 | 0 | 0 | 0, 3 | 0, 87 | 0, 49 | 0 |
| 0, 47 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0, 09 | 0 | 0, 24 | 0 | 0, 05 | 0 |
| 0 | 0, 14 | 0 | 0 | 0, 04 | 0, 07 | 0 |
| 0, 92 | 0, 36 | 0, 02 | 0, 09 | 0, 27 | 0 | 0 |
| 0, 01 | 0 | 0, 06 | 0 | 0 | 0 | 0, 27 |
| 0, 01 | 0 | 0 | 0 | 0 | 0 | 0, 01 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0, 71 | 0 | 0 |
| 0 | 0 | 0, 27 | 0, 08 | 0 | 0 | 0, 33 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0, 03 | 0 | 0, 08 | 0, 14 | 0 | 0 | 0 |
| 0 | 0, 11 | 0, 06 | 0, 02 | 0 | 0 | 0 |
| 0, 01 | 0, 05 | 0 | 0, 01 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0, 12 | 0 | 0 |
| 0, 11 | 0, 03 | 0 | 0 | 0 | 0 | 0, 44 |
| 0, 01 | 0, 01 | 0 | 0 | 0, 11 | 0, 18 | 0 |
| 0, 49 | 0 | 0, 64 | 0, 01 | 0 | 0 | 0, 01 |
| 0 | 0 | 0, 08 | 0, 85 | 0, 01 | 0 | 0 |
| 0, 01 | 0, 02 | 0 | 0 | 0, 03 | 0 | 0 |
| 0 | 0 | 0, 12 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0, 01 | 0, 04 | 0, 26 | 0, 04 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0, 4 | 0 |
| 0, 12 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0, 24 | 0 | 0, 23 |
| 0 | 0 | 0 | 0, 02 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0, 02 | 0 | 0 | 0 |
| 0, 59 | 0 | 0 | 0 | 0 | 0, 68 | 0 |
| 0 | 0, 01 | 0 | 0 | 0 | 1, 48 | 0, 21 |
| 0, 01 | 0 | 0 | 0 | 0, 05 | 0, 69 | 1, 28 |
| 0 | 0 | 0 | 0 | 0, 96 | 0 | 0, 01 |
| 0 | 0 | 0 | 0 | 0 | 0, 79 | 0, 02 |
| 0, 41 | 0 | 0, 06 | 0, 01 | 0 | 0 | 0, 28 |
| 0 | 0 | 0 | 0, 08 | 0, 04 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0, 74 | 0 | 0 | 0 | 0 | 0 |
| 0, 43 | 0, 3 | 0 | 0, 26 | 0 | 0, 02 | 0, 01 |
Calcular su Rango, Desviación Típica y Varianza del quinto año
- La dirección de tránsito de una ciudad del sur de EE.UU. estudia las velocidades que viajan quienes reciben una infracción en una zona de velocidad controlada a 30 millas por hora.
| Velocidad | Frecuencia |
| 42–45 | 25 |
| 46–49 | 14 |
| 50–53 | 7 |
| 54–57 | 3 |
| 58–61 | 1 |
Calcule la desviación típica.
- Calcule la Variación de las calorías por gramo de cereal
| Marca de Cereal | Calorías por gramo de cereal |
| A | 3, 7 |
| B | 3, 6 |
| C | 3, 6 |
| D | 4, 0 |
| E | 4, 0 |
| F | 3, 6 |
| G | 3, 8 |
| H | 3, 7 |
| I | 4, 1 |
| J | 3, 9 |
| K | 3, 9 |
| L | 3, 3 |
| M | 3, 5 |
| N | 3, 6 |
| Ñ | 3, 9 |
| O | 4, 0 |
- Un banco de la India quiere conocer la cantidad de rupias que son suministradas, en un día, por un cajero automático en una zona agrícola
| Rupias | Nº de clientes |
| [0, 20) | 33 |
| [20, 40) | 27 |
| [40, 60) | 19 |
| [60, 80) | 14 |
| [80, 100) | 7 |
Calcular su Rango y Desviación Típica
- Calcular la Varianza y la Desviación Típica de los siguientes datos:
| Intervalo | frecuencia |
| [ 0, 3 ) | 19 |
| [ 3, 6 ) | 24 |
| [ 6, 9 ) | 29 |
| [ 9, 12 ) | 25 |
| [ 12, 15 ) | 28 |
| [ 15, 18 ) | 27 |
| [ 18, 21 ) | 26 |
| [ 21, 24 ) | 22 |
Las medidas de dispersión complementan la descripción del comportamiento y/o características de un conjunto de datos a las medidas de tendencia central.
Ángel Míguez Álvarez