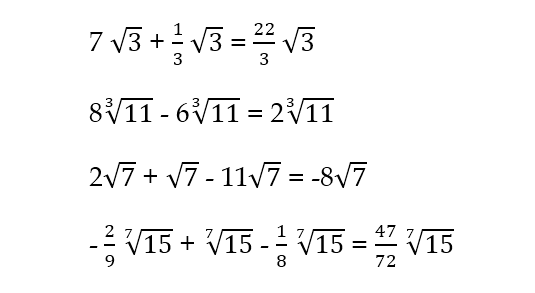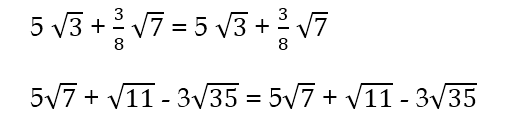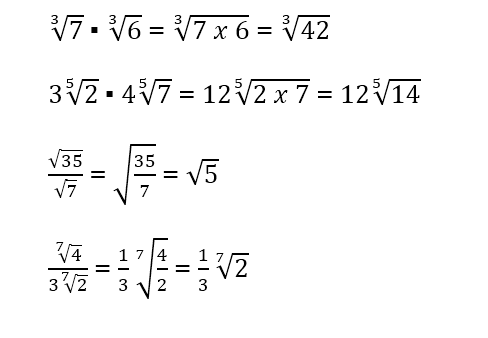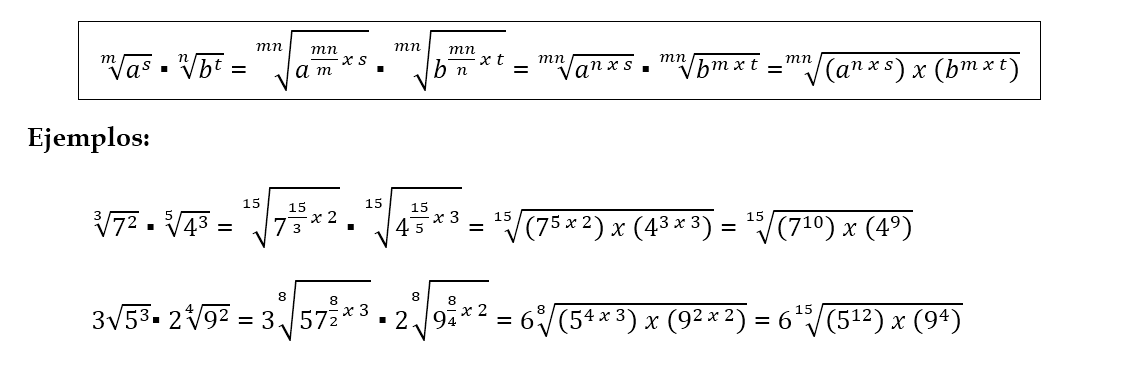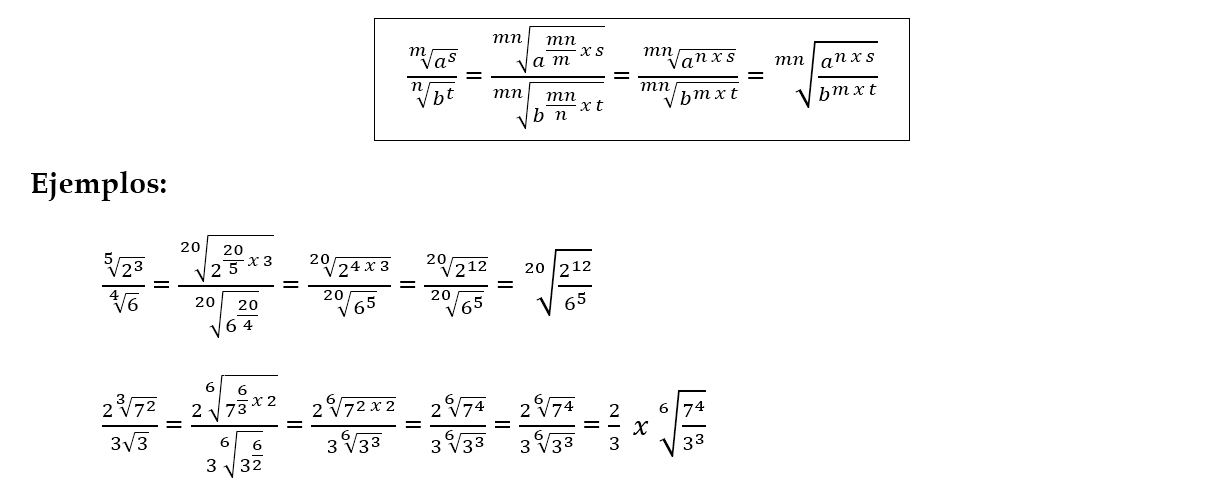Los Números Irracionales son el subconjunto de los Números Reales cuyos elementos no se pueden expresar como una razón, como una fracción de dos Números Enteros. Es decir, pueden ser representados por números con infinitos decimales sin patrón de repetición. Al ver varios ejemplos de números irracionales, podemos notar que se usan en el desarrollo y estudio de la Física, la Química y la Matemática.

Ejemplos de números irracionales

Contra ejemplos

Un número decimal de infinitos decimales puede clasificarse de tres formas distintas

1. Tiene infinitos decimales, los cuales no siguen un patrón de repetición, por ejemplo, el número pi y se denomina número irracional.
2. Tiene infinitos decimales en los que uno o varios números se repiten indefinidamente, por ejemplo 7,5656565656… y se denomina decimal periódico puro.
3. Tiene infinitos decimales, los cuales a partir de cierto número, uno o varios números se repiten indefinidamente, por ejemplo 0,152666666666… y se denomina decimal periódico mixto.

En los dos últimos casos se pueden expresar como una razón de dos números enteros, hallando la fracción generatriz del número decimal.

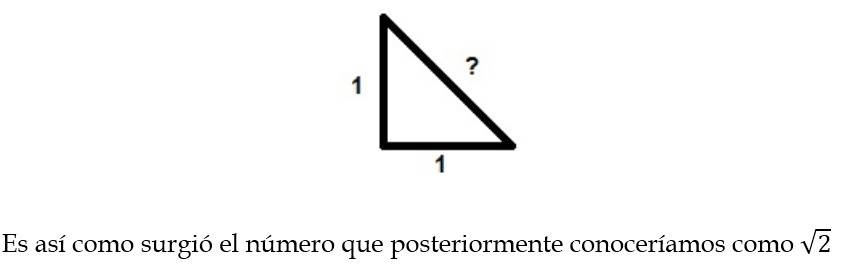
Los Números Irracionales eran denominados por los griegos como los números inconmensurables, es decir, que no se podían medir. Hay dos hipótesis de cómo surgieron estos números y cuáles fueron los primeros irracionales conocidos.

1. Cuando un alumno de Pitágoras intento medir la hipotenusa de un triángulo rectángulo de catetos 1, se percató que no podía encontrar un número conocido por ellos (natural: 1, 2, 3, 4,… o fraccionario) y determinó que la hipotenusa de ese triángulo no se podía medir.
2. La otra hipótesis, la del número áureo, data de 500 años antes de nuestra era. Fue usado y/o mencionado por Phidias, Platón y Euclides. Otros lo ubican 2000 años antes de nuestra era, en referencias de Babilonia y Asiria. Fue usado y recreado por los más destacados personajes del Renacimiento Europeo. Lo cierto es que en el descubrimiento de la proporción áurea, unos usaron el álgebra para establecer el valor de dicho número y se encontraron con esta ecuación:

Adición y Sustracción de Números Irracionales

Estas operaciones cuando se realizan con Números Irracionales semejantes se hacen de la siguiente manera:

Ejemplos:

Cuando las operaciones de adición y/o sustracción se realizan con Números Irracionales que no son semejantes, se dejan indicadas.

Ejemplos:

Salvo que se realicen las operaciones usando una aproximación, tomando dos decimales de los números irracionales.

Multiplicación y División de Números Irracionales

Primero caractericemos los elementos que conforman un número radical.

En algunos libros de texto de Matemáticas al radicando lo denominan como cantidad subradical.

Para multiplicar o dividir dos números radicales de igual índice, se coloca una raíz de igual índice y se multiplican o se dividen los radicandos

Ejemplos:

Para multiplicar dos números radicales de índices distintos m y n, se procede como indicamos en el siguiente esquema:

(En todas estas operaciones las cantidades en el radicando se pueden multiplicar y obtener un número entero)

Para dividir dos números radicales de índices distintos m y n, se procede como indicamos en el siguiente esquema:

(En todas estas operaciones las cantidades en el radicando se pueden simplificar, dividir y obtener un número entero)

En el ámbito escolar los Números Irracionales más usados son los números radicales, el número p, el número e y el número j.

El artículo ha sido realizado por el profesor Licenciado en Matemáticas: Ángel Míguez Álvarez