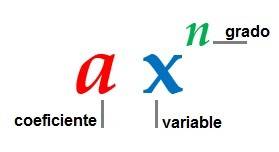
Ejemplos de Polinomios
Los polinomios son una parte fundamental del álgebra y son ampliamente utilizados en muchas ramas de las matemáticas, la física, la ingeniería y otras ciencias aplicadas. Un polinomio es una expresión algebraica que se compone de variables y constantes, combinadas mediante operaciones de suma, resta y multiplicación.
- Por ejemplo, el polinomio 2x³ – 3x² + 5x – 7 es una expresión algebraica que consta de cuatro términos, cada uno de ellos con una variable elevada a una potencia diferente. El primer término, 2x³, tiene una variable x elevada a la tercera potencia y un coeficiente de 2. El segundo término, -3x², tiene una variable x elevada al cuadrado y un coeficiente -3. El tercer término, 5x, tiene una variable x elevada a la primera potencia y un coeficiente positivo de 5. El cuarto término, -7, es una constante sin variable.
Los polinomios permiten modelar situaciones del mundo real. Por ejemplo, en física, los polinomios se utilizan para describir la relación entre la posición, la velocidad y la aceleración de un objeto en movimiento. En economía, los polinomios se utilizan para modelar la oferta y la demanda de bienes y servicios en un mercado. En ingeniería, los polinomios se utilizan para modelar la relación entre la entrada y la salida de un sistema.
Los polinomios tienen propiedades interesantes, como su grado, que es el exponente más alto de la variable en el polinomio. El grado de un polinomio determina su comportamiento a largo plazo, ya que los términos con exponentes mayores dominan sobre los términos con exponentes menores en el límite de la variable hacia el infinito.
Explicación sencilla
Los polinomios son expresiones algebraicas que involucran variables y coeficientes que se combinan mediante operaciones de suma, resta y multiplicación. Los polinomios pueden tener uno o varios términos y se pueden ordenar según el grado de la variable que aparece en ellos.
- Por ejemplo, el siguiente es un polinomio de grado 2:
2x^2 + 3x + 1
En este polinomio, «x» es la variable, «2» es el coeficiente del término de segundo grado, «3» es el coeficiente del término de primer grado y «1» es el término constante.
En los polinomios, la variable puede tomar cualquier valor, y por lo tanto, los polinomios se pueden evaluar para diferentes valores de la variable. También es importante destacar que los polinomios se pueden sumar, restar y multiplicar entre sí de la misma manera que se hace con números ordinarios.
Ejemplos de Polinomios
| f(x) = 2x1 + 1 | p(x) = x2 + 3x1 + 2 |
| g(x) = -3x1 + 5 | q(x) = 2x2 – 5x1 + 1 |
| h(x) = 4x1 – 2 | r(x) = -3x2 + 4x1 – 1 |
| j(x) = x1 + 7 | s(x) = x2 – 2x1 – 3 |
| k(x) = -2x1 – 3 | t(x) = 2x2 + 7x1 – 4 |
| u(x) = x3 – 2x2 + x1 – 3 | A(x) = x4 + 2x3 + x2 + x1 + 1 |
| v(x) = 2x3 + 3x2 – 5x1 + 1 | B(x) = 2x4 – 3x3 + 4x2 – 5x1 + 1 |
| w(x) = -x³ + 4x² – 2x¹ + 7 | C(x) = -x4 + 3x3 – 2x2 + 5x1 – 7 |
| x(x) = 3x3 – 7x² + 5x1 | D(x) = x4 – 4x³ + 6x² – 4x1 + 1 |
| y(x) = -2x3 + 6x² – 4x1 – 1 | E(x) = 3x4 + 2x³ – 5x² + 7x1 – 1 |
| F(x) = -2x4 + 5x³ – 3x² + 4x1– 1 | G(x) = x4 – x³ + 2x² – 3x1 + 5 |
| H(x) = 2x4 + 3x³ – 4x² + 5x1 – 1 | I(x) = -x4 + 2x³ – x² + 3x1 – 2 |
| J(x) = 4x4 – 5x³ + 2x² – x1 + 3 | K(x) = -3x4 – 2x³ + 5x² – 4x1 + 1 |
| L(x) = x4 + x³ – 2x² – 3x1 + 4 | M(x) = 2x4 – 3x³ + x² + 5x1 – 1 |
| N(x) = -x4 + 4x³ – 6x² + 4x1 – 1 | O(x) = x4 – 2x³ + 3x² – 2x1 + 1 |
| P(x) = 3x4 – 7x³ + 5x² – x1 + 2 | Q(x) = -2x4 + 6x³ – 4x² + 3x1 – 1 |
| R(x) = x4 – 3x³ + 4x² – 2x1 + 1 | S(x) = 2x4 + x³ – 3x² + 5x1 – 1 |
| T(x) = -x4 + 2x³ + 3x² – 4x1 + 1 | U(x) = 4x4 – 3x³ + 2x² – x1 + 1 |
| V(x) = -3x4 + 2x³ – x² + 5x1</sup | W(x) = x4 – 4x³ + 7x² – 5x1 + 2 |
| X(x) = 2x4 – 5x³ + 3x² + 4x1 – 1 | Y(x) = -x4 + 3x³ – 2x² + 6x1 – 3 |
¿Cómo es un monomio?
Los monomios también son denominados como: términos de un Polinomio.
Ejemplos:
| 2x | -3y² | 4z³ | 5a⁴ |
| -6b⁵ | 7c⁶ | 8d⁷ | 9e⁸ |
| 10f⁹ | -11g¹⁰ | 12h¹¹ | 13i¹² |
| -14j¹³ | 15k¹⁴ | 16l¹⁵ | 17m¹⁶ |
| 18n¹⁷ | -19o¹⁸ | 20p¹⁹ | -21q²⁰ |
Operaciones aritméticas con Polinomios
Adición de Polinomios
Dados dos Polinomios P(x) y Q(x), para hallar P(x) + Q(x) se debe ordenar ambos polinomios de mayor a menor grado y hallar la suma de los monomios semejantes.
- Ejemplo:
Supongamos que queremos sumar los siguientes dos polinomios: (3x² + 2x – 5) + (2x² – 4x + 7)
Para sumar estos polinomios, simplemente debemos sumar los coeficientes de los términos semejantes, es decir, aquellos términos que tienen la misma variable y el mismo exponente. En este caso, podemos agrupar los términos semejantes de la siguiente manera:
(3x² + 2x – 5) + (2x² – 4x + 7) = (3x² + 2x²) + (2x – 4x) + (-5 + 7)
Ahora, sumamos los coeficientes de cada grupo de términos semejantes:
(3x² + 2x²) = 5x²
(2x – 4x) = -2x
(-5 + 7) = 2
Por lo tanto, la suma de los dos polinomios es:
(3x² + 2x – 5) + (2x² – 4x + 7) = 5x² – 2x + 2
Así, la suma de los dos polinomios es un nuevo polinomio que tiene términos con coeficientes y variables combinados de los polinomios iniciales.
Sustracción de Polinomios
Dados dos Polinomios P(x) y Q(x), para hallar P(x) – Q(x) se debe ordenar ambos polinomios de mayor a menor grado y hallar la resta de los monomios semejantes.
- Ejemplo:
Supongamos que queremos restar los siguientes dos polinomios:
(4x³ – 2x² + x + 5) – (2x³ + 3x² – 2x – 1)
Para restar estos polinomios, es similar a sumar polinomios, lo que debemos hacer es agrupar los términos semejantes. En este caso, podemos agrupar los términos semejantes de la siguiente manera:
(4x³ – 2x² + x + 5) – (2x³ + 3x² – 2x – 1) = (4x³ – 2x³) + (-2x² – 3x²) + (x + 2x) + (5 -(-1))
Ahora, restamos los coeficientes de cada grupo de términos semejantes:
(4x³ – 2x³) = 2x³
(-2x² – 3x²) = -5x²
(x + 2x) = 3x
(5 -(-1)) = 6
Por lo tanto, la resta de los dos polinomios es:
(4x³ – 2x² + x+ 5) – (2x³ + 3x² – 2x – 1) = 2x³ – 5x² + 3x + 6
Así, la resta de los dos polinomios es otro polinomio que tiene términos con coeficientes y variables combinados de los polinomios iniciales.
Multiplicación de Polinomios
Dados dos Polinomios P(x) y Q(x), para hallar P(x) ▪ Q(x) se debe ordenar ambos polinomios de mayor a menor grado y hallar el producto de los monomios usando la propiedad distributiva.
- Ejemplo:
Supongamos que queremos multiplicar los siguientes dos polinomios:
(2x + 3)(x² – 4)
Para multiplicar estos polinomios utilizamos la propiedad distributiva de la multiplicación. Primero multiplicamos el primer término del primer polinomio por cada término del segundo polinomio:
(2x) (x² – 4) = 2x³ – 8x
Luego, multiplicamos el segundo término del primer polinomio por cada término del segundo polinomio:
(3) (x² – 4) = 3x² – 12
Finalmente, sumamos los dos resultados obtenidos para obtener el polinomio resultante:
(2x + 3)(x² – 4) = (2x³ – 8x) + (3x² – 12) = 2x³ + 3x² – 8x – 12
Por lo tanto, la multiplicación de los dos polinomios es:
(2x + 3)(x² – 4) = 2x³ + 3x² – 8x – 12
Así, el polinomio resultante es un nuevo polinomio que tiene términos con coeficientes y variables combinados de los polinomios iniciales.
División de Polinomios
Dados dos Polinomios P(x) y Q(x), para hallar P(x) ÷ Q(x) se debe ordenar ambos polinomios de mayor a menor grado y hallar el Polinomio Cociente C(x), tal que P(x) = Q(x) ▪ C(x), si la división es exacta; o P(x) = Q(x) ▪ C(x) + R(x), donde R(x) sería el Polinomio Residuo de la división de P(x) entre Q(x) si la división no es exacta.
El grado del Polinomio P(x) debe ser mayor o igual al grado del Polinomio Q(x).
El grado del Polinomio R(x) debe ser menor al grado del Polinomio Q(x).
- Ejemplo:
Supongamos que queremos dividir los siguientes dos polinomios:
(3x³ – 4x² + x + 7) / (x – 2)
Para llevar a cabo la división, podemos utilizar el método de la división sintética, que es una forma rápida y eficiente de realizar la división de polinomios cuando el divisor es un polinomio de primer grado.
Primero, escribimos el divisor en la forma (x – 2) y colocamos sus coeficientes en la primera fila de la tabla de división sintética. Luego, colocamos los coeficientes del dividendo en la segunda fila, con ceros en los lugares correspondientes si faltan términos.
2 | 3 -4 1 7
|_______
A continuación, bajamos el primer coeficiente del dividendo y lo escribimos debajo de la línea:
2 | 3 -4 1 7
|_______
3
Luego, multiplicamos el divisor por el número que acabamos de bajar y escribimos el resultado en la tercera fila:
2 | 3 -4 1 7
|_______
3
——-
2 -2 0
Ahora, sumamos los coeficientes de la tercera fila para obtener el primer coeficiente del cociente:
2 | 3 -4 1 7
|_______
3
———
2 -2 0
——–
1 -2 1
Este resultado indica que el primer término del cociente es x² + (-2)x + 1. Para continuar con la división, repetimos los pasos anteriores con el nuevo polinomio que aparece en la última fila de la tabla. Bajamos el siguiente coeficiente del dividendo y lo escribimos debajo de la línea:
2 | 3 -4 1 7
|_______
3
——-
2 -2 0
——-
1 -2 1
2
Luego, multiplicamos el divisor por el número que acabamos de bajar y escribimos el resultado en la cuarta fila:
2 | 3 -4 1 7
|_______
3
———
2 -2 0
———
1 -2 1
2
———
5 -2
Este resultado indica que el segundo término del cociente es 5x + (-2). Como no quedan más términos en el dividendo, la división ha terminado. Por lo tanto, el cociente es:
(3x³ – 4x² + x + 7) / (x – 2) = x² – 2x + 5
y el residuo es -2.
Así, la división de los dos polinomios es:
(3x³ – 4x² + x + 7) / (x – 2) = x² – 2x + 5 – 2/(x-2)