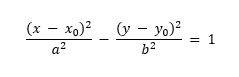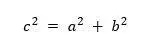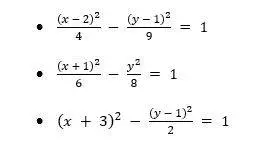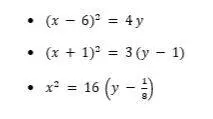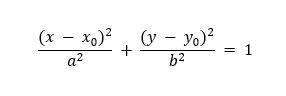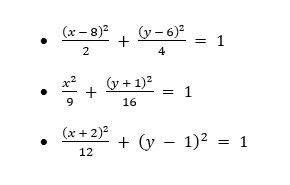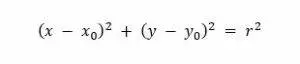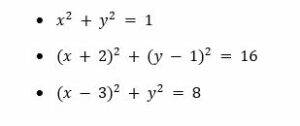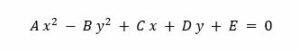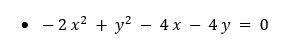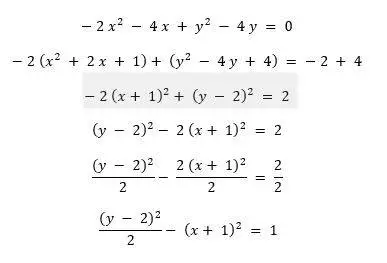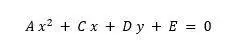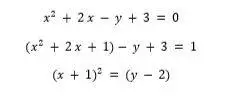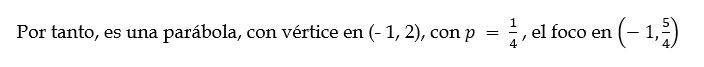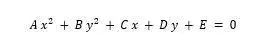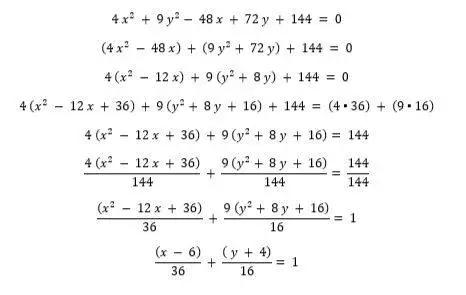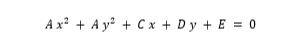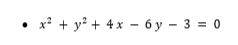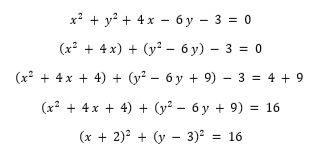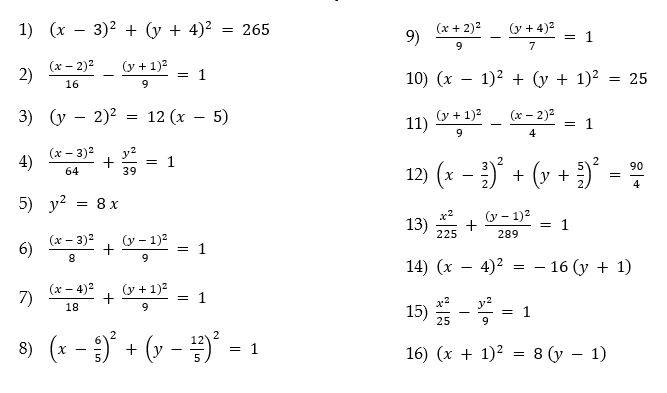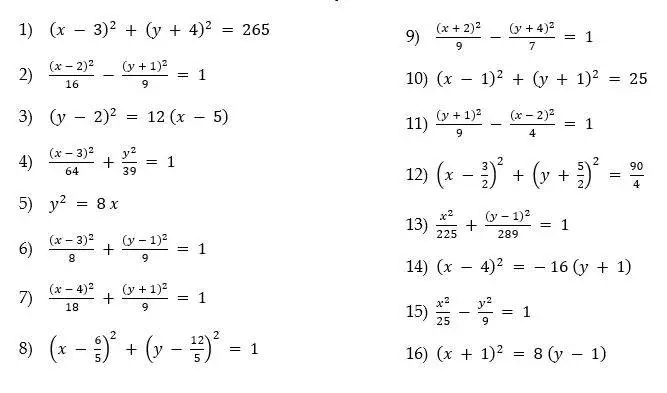Las cónicas o secciones cónicas, son la intersección de un plano con un cono de revolución.

fig. 1 cono de revolución

 

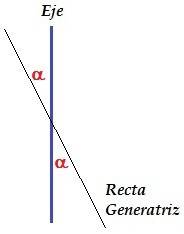
Un cono de revolución es una figura que se crea al hacer girar alrededor de un eje una figura, curva o recta cualquiera, denominada generatriz.

En el caso del cono de revolución se fija un eje, y tomamos una recta generatriz con cierta inclinación a respecto al eje. Al girar esa recta generatriz alrededor del eje se forma un cono de revolución.

fig. 2 eje – recta generatriz

 

El cono de revolución a diferencia del cono que nos enseñaron en la educación básica elemental son dos conos unidos por el vértice.

Al girar la recta generatriz alrededor del eje se genera un cuerpo tridimensional, en este caso un cono de revolución.

 

Secciones cónicas

 

Hipérbola

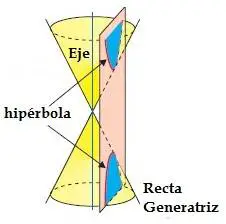
Cuando el plano que intersecta al cono de revolución es equidistante del eje, el plano secciona a ambos conos y genera las dos ramas de la hipérbola.

fig. 3 hipérbola

 

Parábola

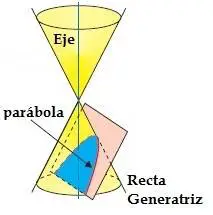
Cuando el plano que intersecta al cono de revolución tiene la misma inclinación respecto al eje que la recta generatriz, el plano secciona solo a un cono y genera la parábola.

fig. 4 parábola

 

Elipse

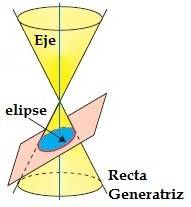
Cuando el plano que intersecta al cono de revolución forma un ángulo agudo con respecto al eje, el plano secciona solo a un cono y genera una elipse.

fig. 5 elipse

 

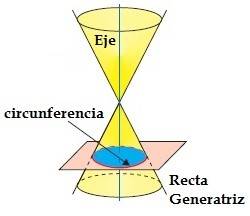
Circunferencia

Cuando el plano que intersecta al cono de revolución forma un ángulo recto (90°) con respecto al eje, el plano secciona solo a un cono y genera una circunferencia.

fig. 6 circunferencia

 

Forma cartesiana de las ecuaciones de las secciones cónicas:

 

Hipérbola:

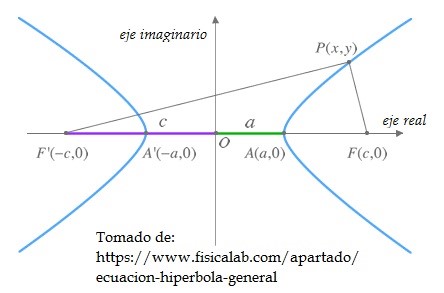
fig. 7 gráfica de una hipérbola

 

(x0, y0) Centro de la hipérbola

a distancia del centro de la hipérbola al vértice, ubicado en el eje real.

c distancia del centro de la hipérbola al foco.

Excentricidad es la que mide la apertura de las ramas de la hipérbola; en el caso de la hipérbola la excentricidad siempre será mayor que uno, e > 1

 

Ejemplos:

 

 

 

 

 

Parábola:

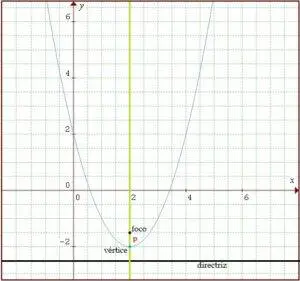
fig. 8 gráfica de una parábola

 

(x0, y0) vértice de la parábola.

p la distancia del vértice al foco de la parábola.

Excentricidad  e = 1. Este elemento relaciona la distancia del foco al vértice con la distancia del vértice a la recta directriz de la parábola.

 

Ejemplos:

Elipse:

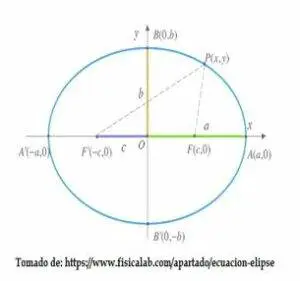
fig. 9 gráfica de una elipse

 

(x0, y0) centro de la elipse.

a distancia del centro de la elipse al vértice del lado mayor, ubicado en el eje focal.

c distancia del centro de la elipse al foco.

b distancia del centro de la elipse al vértice del lado menor, ubicado en el eje vertical.

excentricidad es la que mide la redondez o achatamiento de la elipse; en el caso de la elipse la excentricidad siempre será menor que uno, , mientras el valor de la excentricidad sea menor, más achatada es la elipse y a medida que es mayor se aproxima más a la forma de una circunferencia.

Ejemplos:

Circunferencia:

fig. 9 gráfica de una circunferencia

 

(x0, y0) centro de la circunferencia.

r es la distancia desde el centro de la circunferencia hasta cualquier punto de ésta.

La circunferencia tiene excentricidad cero, ya que no tiene factores de achatamiento o elongación.

 

Ejemplos:

Ecuaciones generales de las secciones cónicas:

 

Hipérbola

Ejemplo:

Usaremos la completación de cuadrados para convertir esta ecuación general en una ecuación cartesiana.

Parábola

Ejemplo:

Usaremos la completación de cuadrados para convertir esta ecuación general en una ecuación cartesiana.

Elipse

Ejemplo:

Usaremos la completación de cuadrados para convertir esta ecuación general en una ecuación cartesiana.

Circunferencia

Ejemplo:

Usaremos la completación de cuadrados para convertir esta ecuación general en una ecuación cartesiana.

Por tanto, es una circunferencia, con centro en (- 2, 3), y radio cuatro, r = 4

Definición de las secciones cónicas como lugar geométrico:

 

Hipérbola

La hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias en valor absoluto a los focos de la misma es constante y mide el doble de la distancia del centro al vértice de la hipérbola (2 a).

La distancia entre sus focos siempre será mayor al doble de la distancia del centro al vértice de la hipérbola (2 a).[1]

 

Parábola

La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto llamado foco y de la recta directriz de dicha parábola.

La distancia del foco a la recta directriz es el doble de la distancia del foco al vértice de la parábola (2 p).[2]

 

Elipse

La elipse es el conjunto de los puntos del plano cuya suma de distancias a los focos es constante y mide el doble de la distancia entre los vértices de la elipse (2 a).

La distancia entre sus focos siempre será menor al doble de la distancia del centro al vértice de la hipérbola (2 a).[3]

 

Circunferencia

La circunferencia es el conjunto de los puntos del plano cuya distancia a un punto llamado Centro es constante y esa distancia recibe el nombre de radio.[4]

 

Ejercicios:

Hallar el tipo de cónica, las coordenadas de centro o vértice y coordenadas de los focos o centro

Hallar las coordenadas de centro o vértice y focos o centro

 

 

 

 

 

 

 

 

 

 

 

Las secciones cónicas han sido útiles para determinar las trayectorias de los planetas y de cometas, la construcción de antenas receptoras, el diseño de focos de iluminación.

 

[1] Ströbl, W. (1 977). Diccionarios Rioduero Matemática. España, Madrid: Ed. Rioduero p. 113

[2] Ströbl, W. (1 977). Diccionarios Rioduero Matemática. España, Madrid: Ed. Rioduero p. 154

[3] Ströbl, W. (1 977). Diccionarios Rioduero Matemática. España, Madrid: Ed. Rioduero p. 85

[4] Ströbl, W. (1 977). Diccionarios Rioduero Matemática. España, Madrid: Ed. Rioduero p. 46