Ejemplos de sistema de coordenadas en el plano y el espacio
El sistema de coordenadas en el plano y en el espacio son formas de ubicar puntos en un espacio bidimensional y tridimensional, respectivamente. En ambos sistemas, utilizamos ejes perpendiculares para ubicar los puntos. En el sistema de coordenadas en el plano, utilizamos dos ejes perpendiculares llamados eje x y eje y. Cada punto en el plano se ubica mediante un par ordenado de números, uno para la coordenada en el eje x y otro para la coordenada en el eje y.
- Por ejemplo, el punto (2,3) se ubica dos unidades hacia la derecha desde el origen en el eje x, y tres unidades hacia arriba desde el origen en el eje y.
En el sistema de coordenadas en el espacio, utilizamos tres ejes perpendiculares llamados eje x, eje y y eje z. Cada punto en el espacio se ubica mediante un triple ordenado de números, uno para la coordenada en el eje x, otro para la coordenada en el eje y, y otro para la coordenada en el eje z.
- Por ejemplo, el punto (1,2,3) se ubica una unidad hacia la derecha desde el origen en el eje x, dos unidades hacia arriba desde el origen en el eje y, y tres unidades hacia adelante desde el origen en el eje z.
El sistema de coordenadas en el plano y en el espacio se utilizan en muchas áreas de la ciencia y la ingeniería, como la física, la geometría y la ingeniería civil. Además, conocer estos sistemas es útil para graficar funciones y visualizar objetos y estructuras en un espacio bidimensional o tridimensional.
En el sistema de coordenadas en el espacio, la distancia entre dos puntos se puede calcular utilizando la fórmula de distancia entre dos puntos en el espacio, que utiliza el teorema de Pitágoras en tres dimensiones.
Explicación sencilla
El sistema de coordenadas es una herramienta matemática que permite describir la posición de un punto en un espacio de dos o tres dimensiones. Es una forma de asignar un par o un trío de números a un punto específico, lo que nos permite ubicar ese punto de manera precisa en un plano o en el espacio tridimensional.
En un sistema de coordenadas bidimensional, también conocido como un plano cartesiano, se utilizan dos ejes perpendiculares para ubicar puntos en un plano. El eje horizontal se llama eje X y el vertical se llama eje Y. El punto donde se cruzan estos dos ejes se llama origen, y se representa con el par ordenado (0,0). Cada punto en el plano se representa mediante un par ordenado (x,y), donde x es la coordenada horizontal y y es la coordenada vertical.
- Por ejemplo, el punto (2,3) se ubica dos unidades hacia la derecha del origen y tres unidades hacia arriba.
En un sistema de coordenadas tridimensional, se utilizan tres ejes perpendiculares: el eje X, el eje Y y el eje Z. El punto donde se cruzan los tres ejes se llama origen, y se representa con el trío ordenado (0,0,0). Cada punto en el espacio tridimensional se representa mediante un trío ordenado (x,y,z), donde x es la coordenada horizontal, y es la coordenada vertical y z es la coordenada perpendicular al plano.
- Por ejemplo, el punto (2,3,4) se ubica dos unidades hacia la derecha del origen, tres unidades hacia arriba y cuatro unidades hacia afuera del plano.
El sistema de coordenadas es una herramienta fundamental en la geometría analítica ya que permite describir la posición, la distancia y el movimiento entre puntos en un espacio de dos o tres dimensiones.
Ejemplos de puntos en el sistema decoordenadas bidimensional
| (0,0) | (1,1) | (-3,5) | (2,-4) |
| (6,0) | (-2,-7) | (3,2) | (-4,3) |
| (5,-2) | (-1,-3) | (-5,4) | (2,6) |
Ejemplos de puntos en el sistema de coordenadas tridimensional
| (0,0,0) | (1,1,-1) | (-3,5,2) | (2,-4,3) |
| (6,0,-2) | (-2,-7,4) | (3,2,-5) | (-4,3,1) |
| (5,-2,-3) | (-1,-3,6) | (-5,4,-2) | (2,6,1) |
Elementos distintivos del Plano Cartesiano
- Un eje denominado abscisas o eje x: es el eje horizontal y divide al plano cartesiano en dos partes, una superior y otra inferior
- Un eje denominado ordenadas o eje y: es el eje vertical y divide el plano cartesiano en dos partes, una derecha y otra izquierda
- Ambos ejes son perpendiculares.
- Punto de Origen de los ejes de coordenadas cartesianas: es el punto donde coinciden los ceros de los ejes coordenados Ox y Oy
- Ambos ejes usan el mismo sistema numérico para la escala de medición, discreto o continuo, , aunque puede variar los elementos que se miden, velocidad y tiempo, volumen y peso.
Coordenadas cartesianas en el plano
Un par ordenado en el plano cartesiano representa las coordenadas de un punto en el plano. Para representar un par ordenado en el plano cartesiano, primero se identifica la coordenada horizontal o eje x, que se representa en el eje horizontal del plano. Luego, se identifica la coordenada vertical o eje y, que se representa en el eje vertical del plano.
Para dibujar el punto correspondiente al par ordenado, se busca la intersección de las dos líneas que representan los ejes x e y en el plano cartesiano. La coordenada horizontal del punto se ubica en el eje x y la coordenada vertical se ubica en el eje y. A partir de la intersección de ambas coordenadas, se dibuja un punto justo en ese punto de intersección.
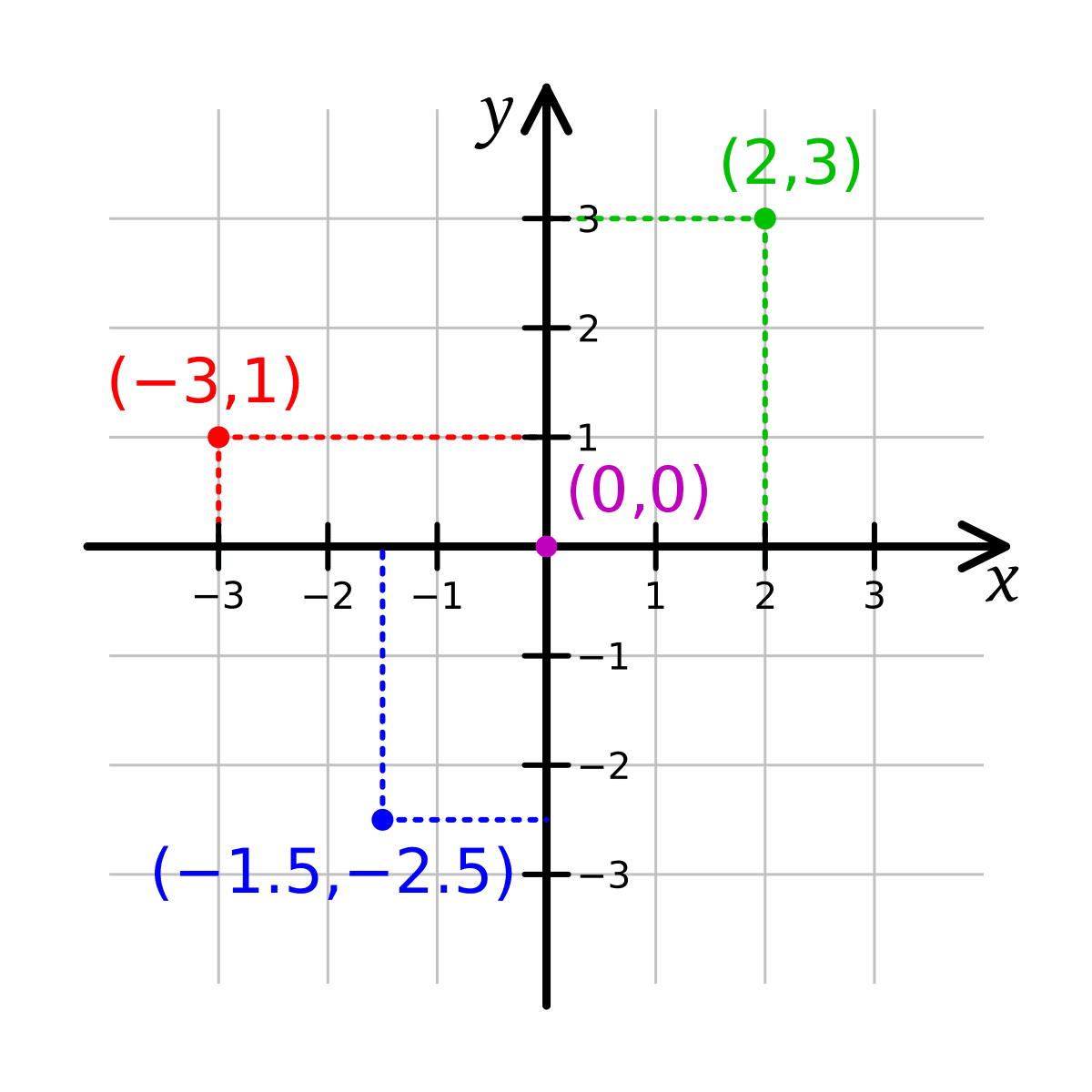
- Por ejemplo, si tenemos el par ordenado (2, 3), primero se ubica el número 2 en el eje x, y luego el número 3 en el eje y. La intersección de las dos coordenadas es el punto donde se dibuja el punto correspondiente al par ordenado (2, 3) en el plano cartesiano.
En la siguiente imagen del plano cartesiano se observa la representación grafica de ese par ordenado (2, 3) así como tambien de los pares ordenados (0, 0), (-3, 1) (-1, 5) y (-2, 5)
Elementos distintivos del Espacio Cartesiano
- Un eje x: es el eje inclinado y divide al Espacio Cartesiano en dos partes, una derecha y otra izquierda.
- Un eje y: es el eje horizontal y divide el Espacio Cartesiano en dos partes, una adelante y otra atrás.
- Un eje z: es el eje vertical y divide el Espacio Cartesiano en dos partes, una arriba y otra abajo.
- Todos los ejes son perpendiculares dos a dos.
- Punto de Origen de los ejes de coordenadas cartesianas: es el punto donde coinciden los ceros de los ejes coordenados Ox, Oy y Oz
- Todos los ejes usan el mismo sistema numérico para la escala de medición, discreto o continuo, , aunque puede variar los elementos que se miden, alto ancho y profundidad, volumen, peso y tiempo.
Coordenadas cartesianas en el espacio
Para representar un punto en el espacio cartesiano, se utiliza un trío ordenado de números reales (x, y, z), donde el primer número representa la coordenada horizontal, el segundo número representa la coordenada vertical y el tercer número representa la coordenada en la profundidad.
Para dibujar el punto correspondiente al trío ordenado, se ubica la coordenada horizontal (x) en el eje x, la coordenada vertical (y) en el eje y y la coordenada en la profundidad (z) en el eje z. La intersección de las tres coordenadas es el punto donde se dibuja el punto correspondiente al trío ordenado (x, y, z) en el espacio cartesiano.
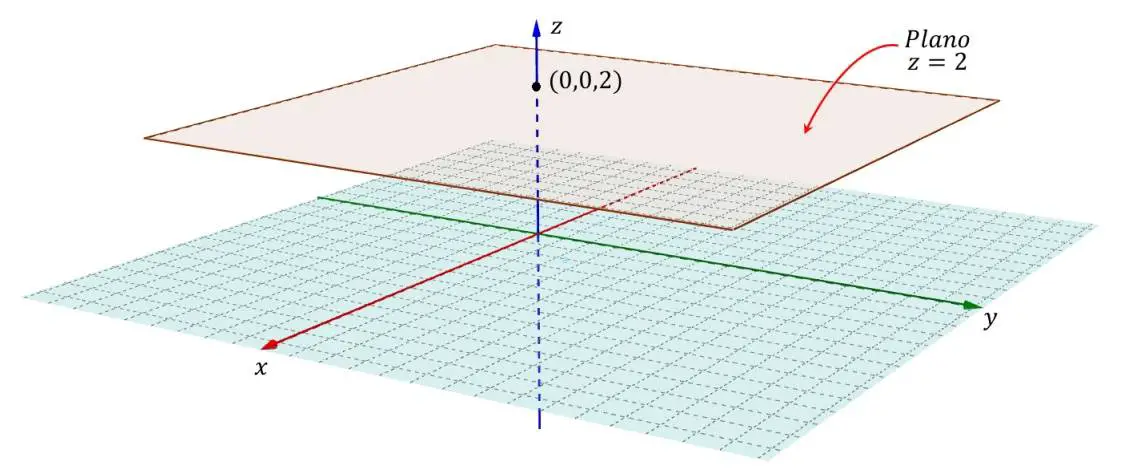
- Por ejemplo, si tenemos el trío ordenado (0, 0, 2), primero se ubica el número 0 en el eje x, luego el número 0 en el eje y y finalmente el número 2 en el eje z. La intersección de las tres coordenadas es el punto donde se dibuja el punto correspondiente al trío ordenado (2, 3, 4) en el espacio cartesiano.
En la siguiente imagen del plano cartesiano se observa la representación grafica de ese trío ordenado (0, 0, 2