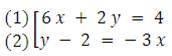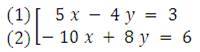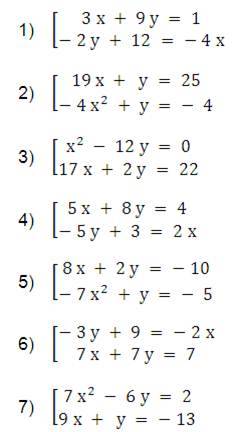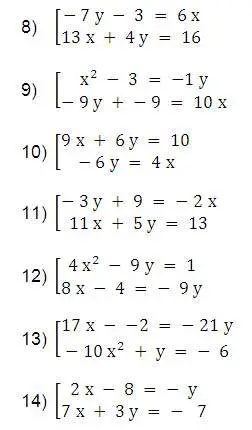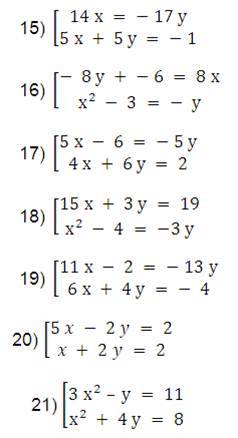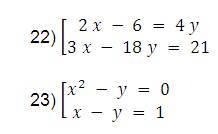30 Ejemplos De Sistemas De Ecuaciones
Un sistema de ecuaciones es un arreglo de ecuaciones que busca determinar su punto de intersección y/o su compatibilidad.
Los sistemas de ecuaciones pueden tener dos o más ecuaciones, lineales o de cualquier grado y dos o más incógnitas.
Tipos de Sistemas de Ecuaciones
Un sistema de ecuaciones cualquiera debe tener, al menos, el mismo número de ecuaciones que de incógnitas. De lo contrario, si tiene menos ecuaciones que incógnitas, una o más de las incógnitas debe expresarse en función de otra o de las otras.
En casos así se debe analizar los intervalos de solución en caso de que sea posible hallarlo.
Cuando el sistema de ecuaciones tiene el mismo número de ecuaciones que de incógnitas, entonces se presentan estos tipos:
- Sistema de ecuaciones compatible determinado, el cual es uno en el que la solución a las incógnitas es única e indica dónde se interceptan las gráficas de las ecuaciones en estudio.
- Sistema de ecuaciones compatible indeterminado, en este caso las gráficas de las ecuaciones son idénticas. Aunque sus expresiones algebraicas sean diferentes en forma. En este caso cualquier valor es solución, tiene infinitas soluciones.
- Sistema de ecuaciones incompatible, es el caso en el que las gráficas de las ecuaciones no se interceptan en ningún punto. En el caso de ecuaciones lineales en el plano las gráficas son rectas paralelas.
¿Cómo se resuelve un sistema de ecuaciones?
En la matemática escolar se suelen plantear sistemas de ecuaciones de dos, tres y hasta cuatro ecuaciones. Con el uso de matrices se suelen plantear hasta de cinco ecuaciones.
Pero, con el uso de sistemas informáticos se pueden plantear procedimientos algorítmicos de cualquier cantidad de ecuaciones.
Tenemos tres métodos de uso generalizado en el ámbito escolar:
Método de igualación
Consiste en despejar de dos ecuaciones una misma incógnita, luego se igualan las dos expresiones y se calcula el valor de la otra incógnita.
Ejemplo:
Por tanto, el sistema de ecuaciones es compatible determinado, la solución es (43/11 , 3/11)
Método de sustitución
Consiste en despejar en una de las ecuaciones una incógnita, luego se sustituye el valor de esa incógnita en la otra ecuación y se despeja la incógnita que queda.
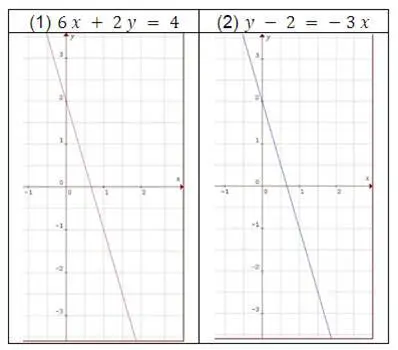
Por tanto, el sistema de ecuaciones es compatible determinado, la solución es (1,2)
Método de reducción
Consiste en realizar operaciones válidas matemáticamente en las ecuaciones que permitan despejar una incógnita. Luego se repite el procedimiento para despejar la otra incógnita.
Ejemplo:
Multiplicamos la segunda ecuación por – 2 y la sumamos a la primera ecuación, remplazándola.
De acá se deduce que
Multiplicamos la primera ecuación por y la sumamos a la segunda ecuación, remplazándola.
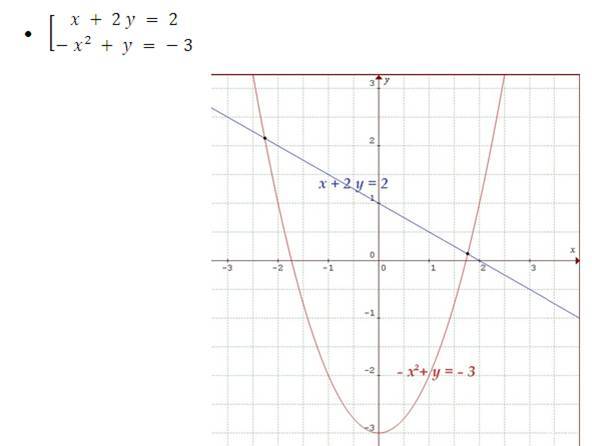
Ejemplo de un sistema de ecuaciones compatible indeterminado
Hagamos la representación gráfica de ambas ecuaciones:
Como se puede apreciar ambas ecuaciones tienen la misma representación gráfica, lo que nos permite afirmar que ambas ecuaciones son idénticas, y por ello cualquier punto (x, y) que sea solución de la ecuación (1) es también solución de la ecuación (2), de ahí la indeterminación de la solución solicitada.
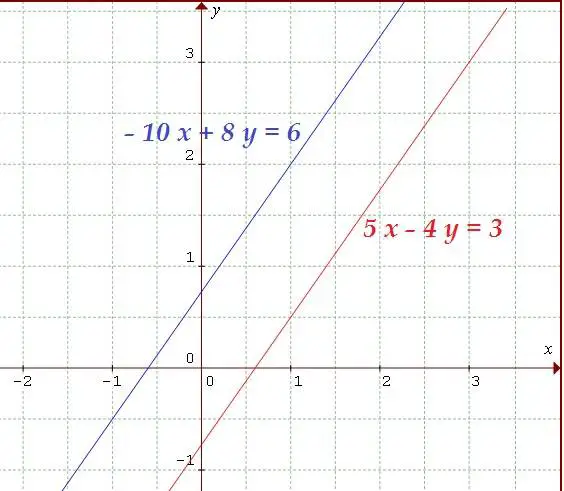
Ejemplo de un sistema de ecuaciones incompatible
Hagamos la representación gráfica de ambas ecuaciones:
No hay solución posible dado que ambas ecuaciones no tienen ningún punto en común por ser paralelas. Por eso el sistema es incompatible.
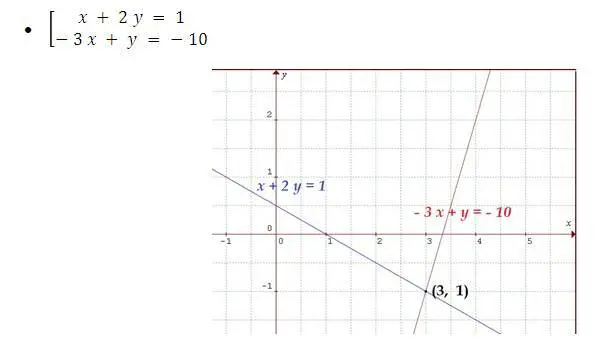
Ejemplos gráficos de sistemas de ecuaciones compatibles
Sistema compatible determinado, solución (3, – 1)
Ejemplos de sistemas de ecuaciones
Ejercicios
- Resuelve los sistemas de ecuaciones pares de los ejemplos anteriores y determina el o los puntos solución
- Grafica en el plano los sistemas de ecuaciones impares de los ejemplos anteriores y determina el o los puntos solución
Los sistemas de ecuaciones de múltiples variables son usados para modelar procesos reales en economía, industria, comercio y ciencia.
Ángel Míguez Álvarez