Ejemplo Algoritmo de Euclides
El algoritmo de Euclides es un método antiguo y eficiente para calcular el máximo común divisor (MCD) de dos números enteros. El MCD de dos números es el número más grande que puede dividir exactamente a ambos números sin dejar residuo. El algoritmo de Euclides se basa en la propiedad de que el MCD de dos números no cambia si se resta el menor de ellos al mayor.
Pasos Algoritmo de Euclides
Te explicamos los pasos del algoritmo de Euclides para calcular el MCD de dos números enteros positivos a y b:
- Comprueba si alguno de los números es cero. Si a o b es cero, el MCD es el número distinto de cero. Por ejemplo, si a = 0 y b = 5, entonces MCD(a, b) = 5.
- Si ambos números son distintos de cero, divide el número mayor (a) por el número menor (b) y anota el residuo (r). Es decir, calcula r = a % b (el operador % indica el resto de la división entera).
- Si el residuo (resto) (r) es cero, el MCD es el divisor (b). En este caso, termina el proceso y devuelve b como el MCD.
- Si el residuo (resto) (r) no es cero, reemplaza a por b y b por r, y repite los pasos 2 y 3 hasta que el residuo sea cero.
Veamos un ejemplo concreto para calcular el MCD(48, 18):
- 48 % 18 = 12 (dividimos 48 entre 18 y el residuo es 12)
- 18 % 12 = 6 (ahora dividimos 18 entre 12 y el residuo es 6)
- 12 % 6 = 0 (finalmente, dividimos 12 entre 6 y el residuo es 0)
Como el residuo es cero, el MCD(48, 18) es 6.
El algoritmo de Euclides es muy eficiente, incluso para números muy grandes, y se utiliza ampliamente en matemáticas y ciencias de la computación.
Algoritmo de Euclides extendido
Los procedimientos para calcula el Máximo Común Divisor para números enteros relativamente grandes puede ser engorroso.
Con base en el Algoritmo de la División diseñado por los griegos, se creó una forma que facilita dicho cálculo.
Sean a y b dos números naturales cualesquiera con a y b ≠ 0 y a > b, podemos representarlos así:
a = q1 x b + r1, con b > r1 ³ 0 y q1, r1 números naturales
Si r1 ≠ 0, se procede a dividir el divisor entre el resto
b = q2 x r1 + r2, con r1 > r2 ³ 0 y q2, r2 números naturales
Este paso se repite hasta que el residuo = 0
r1 = q3 x r2 + r3, con r2 > r3 ³ 0 y q3, r3 números naturales
…
rn = qn+2 x rn+1 + 0, con rn+2 = 0 y qn+2 un número natural
El MCD (a, b) = rn+1
Este algoritmo permite, además de encontrar un Máximo Común Divisor de dos números enteros, expresarlo como la combinación lineal, mínima, de estos números.
Calculemos el MCD (703, 399) usando este algoritmo
703 = 1 x 399 + 304
399 = 1 x 304 + 95
304 = 3 x 95 + 19
95 = 5 x 19 + 0
De aquí tenemos que MCD (703, 399) = 19
Ejemplos
- ¿Cuál es el MCD (352, 105)?
352 = 3 x 105 + 37
105 = 2 x 37 + 31
37 = 1 x 31 +6
31 = 5 x 6 + 1
6 = 6 x 1 + 0
El MCD (352, 105) = 1 → entonces los números naturales 352 y 105 son primos relativos
- ¿Cuál es el MCD (49 896, 26 460)?
El MCD (49 896, 26 460) = 756
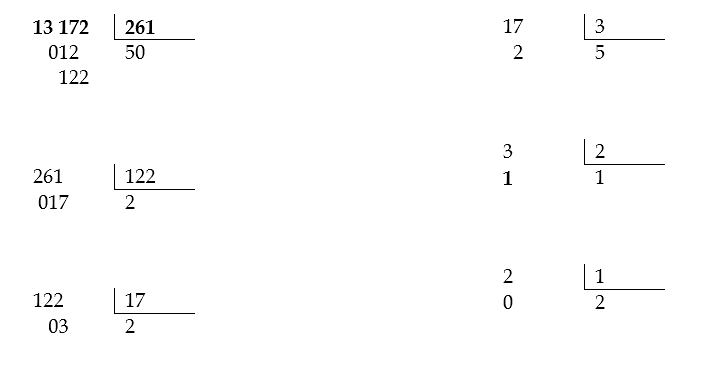
- ¿Cuál es el MCD (13 172, 261)?
El MCD (13 172, 261) = 1 → entonces los números naturales 13172y 261 son primos relativos
- ¿Cuál es el MCD (11 823, 11 172)?
11 823 = 1 x 11 172 + 651
11 172 = 17 x 651 + 105
651 = 6 x 105 + 21
105 = 5 x 21 + 0
El MCD (11 823, 11 172) = 21
El artículo ha sido realizado por el profesor Licenciado en Matemáticas: Ángel Míguez Álvarez