Ejemplos De Inecuaciones En El Plano
Las inecuaciones en el plano son una herramienta matemática esencial para representar una amplia variedad de situaciones en las que se establece una relación de desigualdad entre dos variables.
En el contexto de las inecuaciones en el plano, es común representar las variables en un sistema de coordenadas cartesianas, donde el eje horizontal representa una variable y el eje vertical representa la otra variable. Las inecuaciones en el plano se pueden representar gráficamente como regiones sombreadas en el plano que cumplen la relación de desigualdad.
- Por ejemplo, considera la inecuación 2x + 3y < 6. Podemos representar esta inecuación en el plano cartesiano trazando la línea recta 2x + 3y = 6, y luego sombreando la región del plano que está por debajo de la línea. Esto se debe a que cualquier punto en la región sombreada tendrá coordenadas (x,y) que satisfacen la desigualdad 2x + 3y < 6.
Las inecuaciones en el plano tienen una gran cantidad de aplicaciones en la vida cotidiana y en una amplia variedad de disciplinas, desde la economía y las finanzas hasta la ingeniería y la física.
- Por ejemplo, las inecuaciones pueden utilizarse para modelar restricciones en la producción y el consumo, límites en la capacidad de producción o consumo, y para predecir el comportamiento de sistemas físicos.
Explicación sencilla
Las inecuaciones en el plano son como las reglas que usamos para comparar dos cosas. Imagina que tienes dos cajas de juguetes, una con 5 juguetes y otra con 10 juguetes. Podemos escribir la inecuación «5 < 10» para decir que la primera caja tiene menos juguetes que la segunda.
En el plano, las inecuaciones nos permiten comparar dos variables que están representadas en un sistema de coordenadas cartesianas.
- Por ejemplo, podemos tener una inecuación que dice «x + y < 10», lo que significa que la suma de las coordenadas x e y de cualquier punto en el plano debe ser menor que 10.
Para visualizar esto, podemos dibujar una línea recta que representa la igualdad «x + y = 10», y luego sombrear la región del plano que está por debajo de la línea. Cualquier punto en esta región satisface la inecuación.
Ejemplos de Inecuaciones en el plano
| 2x + 3 < 7 | 4y – 6 > 10 | x2 – 9 < 0 | 3x + 4y ≥ 12 |
| y/2 – 1 ≤ 3 | 5x – 2y > 8 | 2x2 + x – 6 ≥ 0 | 3(x – 2) ≤ 9 |
| 4y2 + 3y – 2 < 5y2 + 7 | 2x + 3y < 5x – 2y + 1 | x – 4 ≥ -3 | 6x + 5 < 8x – 4 |
| 3x2 – 2x + 1 > 0 | 2(x – 3) < 10 | 4y + 3 ≤ 6y – 2 | 5x2 – 2x – 7 > 0 |
| 2(x + 1) > x + 4 | 3y – 4x ≤ 6 | x2 – 6x + 9 ≥ 0 | 2y + 3x < 10y – 5x |
| 4x – 2 > 2x + 5 | 3y2 + 2y – 1 ≤ 4y2 + 5y | 5(x – 2) > 15 | 2x + 3y- 4 < 0 |
| x2 + 2x – 3 ≤ 0 | 2y + x > 5 | 3x – 4y > 2x + 1 | 4y2 – 5y + 2 < 3y2 + 4y + 7 |
| 2x + 3y > 6 | 3(x – 1) < 5x – 2 | 6x + 5 > 4x + 12 | 4y2 – 5y + 2 > 3y2 + 4y + 7 |
| 2(x2 – 3x + 1) < 2x – 1 | y/4 + 2 < 5 | 3x + 2y ≤ 12 | 2x2 – 3x – 2 < x2 + 4x + 1 |
| 5y – 3x > 2y + 7x | 4x – 3 > x + 5 | 2y2 – y – 3 ≤ y2 + 2y – 5 | x2 + 6x + 9 > 0 |
¿Cómo se resuelve una inecuación en dos dimensiones?
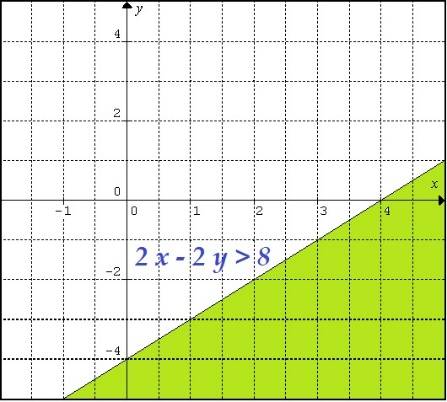
Utilicemos un ejemplo para entender cómo se resuelve una inecuación en dos dimensiones. La inecuación 2x – 2y > 8 es una desigualdad lineal en dos dimensiones, que define una región del plano cartesiano. Para resolverla, primero debes graficar la recta correspondiente a la ecuación 2x – 2y = 8, que es la recta que separa el plano en dos regiones: la región en la que la desigualdad es verdadera y la región en la que es falsa.
La recta correspondiente a la ecuación 2x – 2y = 8 se puede escribir en forma explícita despejando y:
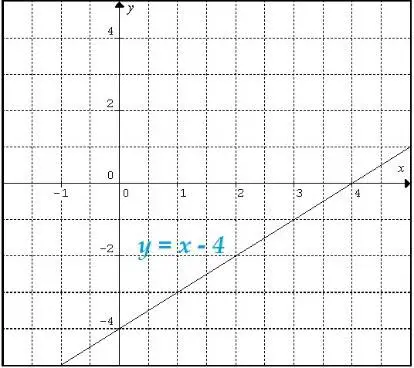
y = x – 4
Representamos en el plano la recta y = x – 4
El plano se divide en la parte superior a la recta y = x – 4 y otra inferior.
Tomamos un punto de la parte superior y evaluamos, tomemos el punto (1, 0) y lo reemplazamos en la inecuación:
y < -4 + x
0 < -4 + 1
0 < -3
Esta respuesta es falso ya que cero (0) no es menor que – 3
Por tanto, esta inecuación se cumple para todos los valores debajo de la recta y = x – 4