25 Ejemplos de Funciones dadas en forma de tabla
Las funciones dadas en forma de tabla es la forma más usual de establecer relaciones entre conjuntos de datos que cumplan los requisitos para ser una función y están presentes en la ingeniería, física, química, medicina, biología, educación, geografía y en todos los fenómenos de la vida.
Ejemplos:
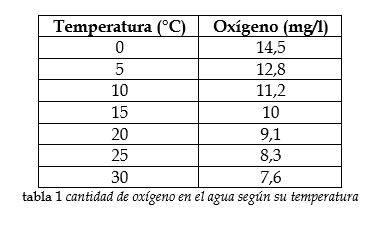
- Cantidad de oxígeno disuelta en el agua en correspondencia con la temperatura de la misma.
- Tabla que predice la posición final de una partícula, en un movimiento lineal, con base en la posición inicial
A simple vista el comportamiento de la cantidad de oxígeno en el agua con base en la temperatura de la misma no responde al de alguna función matemática conocida.
¿Cómo hallar la cantidad de oxígeno en el agua a 23°C?
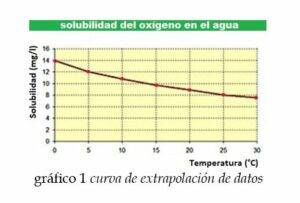
Usando un gráfico como el que se muestra abajo podemos predecir la solubilidad del oxígeno en el agua a esa temperatura.
En este caso se pueden algebrizar los datos y hallar la ecuación que determina la posición de la partícula, con base en su posición inicial.
Construcción de tablas de datos
La investigación en ciencias naturales y sociales requiere de datos que sustenten sus teorías, análisis, proyecciones y predicciones. Para ello es importante, describir adecuadamente el origen de los datos y los métodos de recolección.
El paso siguiente a la recolección es su organización. Se acostumbra construir una tabla en la que se colocan de manera ordenada los datos obtenidos y se señala qué valores representan dichos datos.
Ejemplos:
- Alturas sobre el nivel del mar
- Capacidad de los recipientes usados
- Clima
- Crecimiento poblacional
- Distancias recorridas por los grupos desplazados
- Extensión territorial de ubicación de las etnias
- Frecuencia cardíaca
- Localización geoespacial de las poblaciones
- Número de habitantes
- Número de miembros de la familia
- Porcentaje de células enfermas
- Tamaño de las partículas
- Temperaturas atmosféricas
- Temperatura de la sustancia
- Tipos de suelo
- Topografía del terreno
- Usos del suelo
- Velocidad del objeto
- Velocidad del viento
- Volumen de agua
- Votos emitidos
Interpretación de los datos de la tabla
Una vez construidas las tablas de datos se procede a analizar si existe un patrón conocido que permita explicar los datos presentados, para estimar datos no presentados en las tablas pero que son requeridos o para predecir datos en casos no estudiados.
Acá entra en juego las herramientas matemáticas:
- ¿Se comportan los datos como una función matemática conocida (lineal, exponencial, cuadrática, logarítmica, métodos estadísticos, etc.)?
- ¿Es posible construir una representación gráfica lineal con base en correlaciones entre los datos?
- ¿Es posible construir una representación gráfica curvilínea con base en correlaciones entre los datos?
- ¿Es posible hallar tipos de interpolación entre datos que permitan hallar datos no registrados?
- ¿No es posible relacionar o correlacionar las variables por su carácter aleatorio?
Es por ello que toda investigación actual, en cualquier área requiere del auxilio de un matemático o un estadístico que permita hacer todos los estudios pertinentes a los datos encontrados.
Funciones a trozos
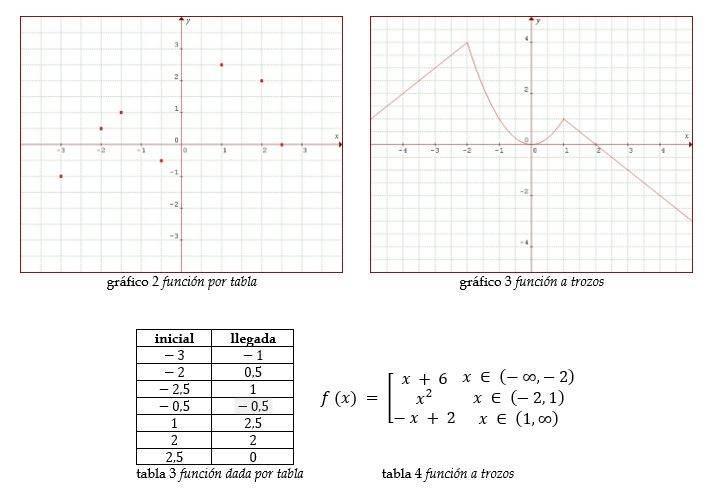
Las funciones a trozos se asemejan a las funciones dadas en forma de tabla en lo siguiente, las segundas están claramente definidas en un punto en particular, con la tabla tenemos entonces una función definida en varios puntos.
Las funciones a trozos están claramente definidas en un intervalo, lo que la convierte en una función definida por intervalos que pueden llegar a convertirse en puntos.
Ejemplos:
Ejemplos:
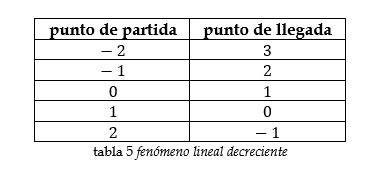
- Fenómeno lineal decreciente
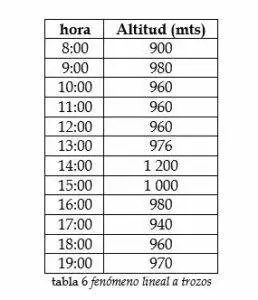
- En un recorrido por la cordillera de la costa en el parque nacional Wuaraira Repano se registran los siguientes datos:
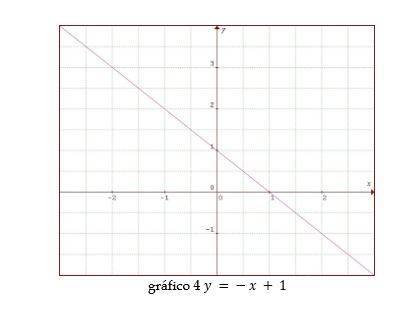
Como se puede apreciar este fenómeno su puede interpretar como un fenómeno donde sus datos decrecen de manera lineal.
Si se quiere hallar el comportamiento de este fenómeno, cuando el punto de partida vale , observando la gráfica podemos determinar que le corresponde en el punto de llegada el valor .
De igual manera, si fuera de interés en el estudio de este fenómeno, hallar un valor extremo, por ejemplo, si el valor del punto de partida fuera 20, usando la función que permite predecir este valor obtenemos que en Þ
Con este ejemplo hemos convertido, haciendo uso de una linealidad supuesta, una función definida en algunos puntos por una tabla en una definida a trozos.
En el caso analizado es factible hacer esta aproximación dado que un sendero montañoso nunca es lineal y esta nivelado a la misma altitud, pero si es factible que su variación sea mínima, menor de medio metro, lo que permite hacerla “lineal”.