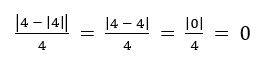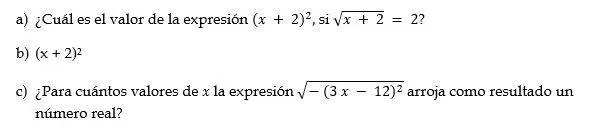La Matemática es una ciencia de la que hay miles de expresiones clásicas entre familias, empleadores, académicos y personas de la calle. De la Valoración de esa ciencia han surgido las Olimpiadas Matemáticas con la finalidad de:

• Detectar estudiantes con inclinaciones al estudio de la matemática.
• Estimular a los alumnos desde temprana edad para el estudio de las matemáticas.
• Presentar las matemáticas escolares desde un punto de vista novedoso, divertido y retador.
• Proporcionar a los maestros un banco de problemas originales, ingeniosos y de variada dificultad para su uso en el aula de matemáticas.

¿Qué es un problema matemático?

Asumimos que un problema matemático es una situación real o ficticia que reta la comprensión conceptual, y no solamente los conocimientos de un tema tratado en la actividad de aprendizaje de matemática.

Exige una reestructuración en la manera de abordar la situación planteada y de los límites de los procedimientos conocidos, y busca generar conexiones sobre conocimientos variados. Un problema no tiene condición temporal, se puede resolver rápidamente, o no conseguírsele nunca su solución”[1].

¿Cómo se resuelve un problema matemático?

En 1944 George Pólya escribió un libro donde planteó cómo plantear y resolver problemas[2] y desde entonces han surgido otras propuestas, que en nuestra opinión, son variantes de la propuesta original de Pólya.

Nosotros hemos venido usando en estas lecciones el siguiente esquema para abordar la solución de un problema matemático, derivado de la propuesta del famoso matemático húngaro ya citado y que mostramos a continuación:

1. Datos del problema
2. Plan para resolverlo
3. Ejecución del plan
4. Verificación de los resultados
5. Visión retrospectiva

Ejemplos de problemas Competenciales en Matemática

• Factorice el polinomio x³ – x² – 4x + 4

Datos del problema:  x³ – x² – 4x + 4

Plan para resolverlo: factorizar el polinomio usando el factor común

Ejecución del plan: x³ – x² – 4x + 4 = x² (x – 1) – 4x + 4 =

x² (x – 1) – 4 (x – 1) = (x² – 4) (x – 1) = (x – 2) (x + 2) (x – 1)

entonces x³ – x² – 4x + 4 = (x – 2) (x + 2) (x – 1)

Verificación de los resultados: multiplicando los tres binomios (x – 2) (x + 2) (x – 1)  obtenemos el polinomio de grado tres x³ – x² – 4x + 4

Visión retrospectiva:    tenemos tres factorizaciones clásicas:

• Factor común
• Binomio cuadrado perfecto
• Suma por su diferencia

En este caso el binomio cuadrado perfecto[x (x² – x – 4) + 4] no tiene solución entera, habría de calcularse la √17, lo que hace ese camino inviable. Por ello, primero obtuvimos el factor común  x² y -4 , para luego volver a usar el factor común del binomio (x – 1)  para concluir con Suma por su diferencia con el binomio (x² – 4) .

Ejercicios:

1. Cuál es el resultado de simplificar la expresión
2. Cuál es el valor de si  a⁴ + b⁴   si   a + b = 1   y    a² + b² = 2

Uno de los nudos clave en la traducción de un problema escrito en lenguaje natural es poder escribirlo en el lenguaje simbólico propio de la matemática.

• Si se suma dos tercios de un número a 24 se obtiene el doble del número. ¿Cuál es el número?

Datos del problema:     tenemos un número desconocido que llamaremos x, tenemos dos tercios de dicho número, es decir, 2/3 x  y tenemos el número 24 y el doble del número que deseamos calcular, es decir, 2x

Plan para resolverlo: resolveremos entonces la ecuación 2/3 x + 24 = 2x

Ejecución del plan: 2/3 x + 24 = 2x  ⇒ 2/3 x – 2x = -24

⇒ 2x – 6x = -72  ⇒ -4x = -72  ⇒  x = 18

entonces el número buscado es 18

Verificación de los resultados: dos tercios de 18 es 12 y si a 12 le sumamos 24 obtenemos 36, que es el doble del número 18

Visión retrospectiva:    traducción:

• Dos tercios de un número, primero el número desconocido lo denominamos x, entonces dos tercios de este es el número desconocido multiplicado por 2/3
• Le sumamos 24, esta parte parece obvia
• El doble del número, es 2 x

Ejercicios:

1. Airam tiene 7x + 1 rupias y Yasury tiene x + 7 rupias. Si Airam tiene 30 rupias más que Yasury ¿Cuánto dinero tiene Yasury?
2. Varias cabras se comen la yerba de un patio en tres días. Si hubiese 3 cabras más se comerían toda la yerba del patio en dos días. Suponiendo que todas las cabras comen la misma cantidad ¿en cuánto tiempo se comería toda la hierba de ese patio una sola cabra?
3. Si x ≠ 0 ¿para cuales valores de x la expresión  es un entero positivo?

Datos del problema: Si x ≠ 0, un número entero positivo es un número estrictamente mayor que cero y obviamente entero, 1, 2, 3, 4, 5, 6…, como podemos apreciar es el conjunto de los números Naturales Ν

Plan para resolverlo: evaluaremos la expresión asignándole valores a x

Ejecución del plan:     si x > 0

La expresión x – |x| = 0 ya que restaríamos dos números iguales y por tanto la expresión

si x < 0

La expresión  x – |x| < 0 y por tanto la expresión |x – |x| > 0 de donde se obtiene que la expresión

entonces la expresión  no será un entero positivo para ningún valor de x

Verificación de los resultados: podemos valuar la expresión  para valores positivos y para valores negativos

Si x = -3

Si x = 4

Visión retrospectiva:    Hemos comprobado que dadas las condiciones del problema (x ≠ 0)  , para cualquier valor positivo el resultado es cero y para cualquier valor negativo el resultado es positivo. Por tanto, no importa el valor que tomemos no obtendremos un número natural como resultado.

Ejercicios:

Como puedes observar hay una infinidad de problemas que se pasean por los más variados enfoques del álgebra escolar, te invitamos a buscar más problemas tipo competencia, tipo olimpíadas que conseguirás en libros y en la red.

Te sugerimos revisar este: https://librosparaestudiarmatematicas.wordpress.com/2016/10/16/un-desafio-a-la-juventud-ii/

[1] Míguez, Á. (2003) “Caracterización de los ejemplos, ejercicios,  y preguntas usados en el aula, en los libros de texto y demás materiales escritos de matemática en el contexto escolar venezolano”. En: Revista Educación y Pedagogía. Medellín: Universidad de Antioquia, Facultad de Educación. Vol. XV, No. 35, (enero-abril).

[2] Polya, G. (1 969). Cómo plantear y resolver problemas. México: Trillas.