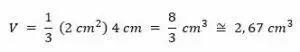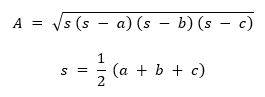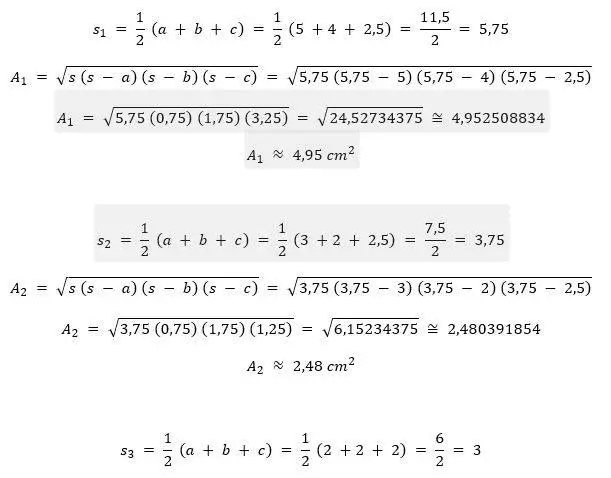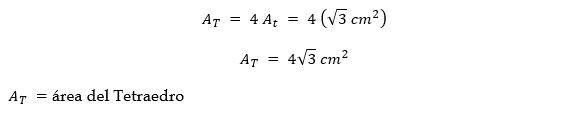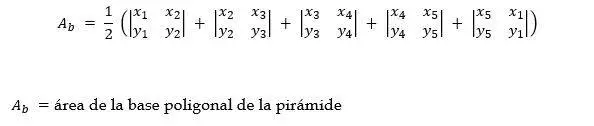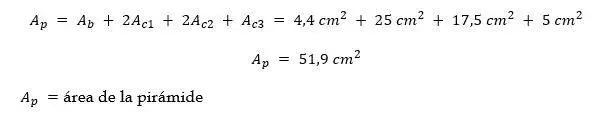El volumen y el área de una pirámide es el cálculo que se efectúa en un poliedro que cuenta con una base en forma de un polígono cualquiera y que el resto de sus caras son triángulos que tienen un vértice común denominado vértice de la pirámide.

Hay pirámides cuya base es un polígono regular o irregular, un polígono cóncavo o convexo, por tanto, hay infinitas pirámides.

Ejemplos:

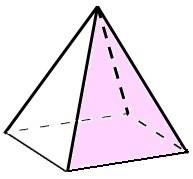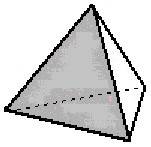
fig. 1 pirámide base triángulo regular	fig. 2 pirámide base cuadrada
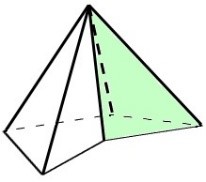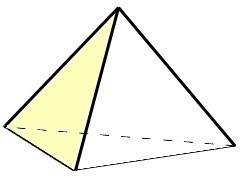
fig. 3 pirámide base triangular	fig. 4 pirámide base pentagonal cóncava

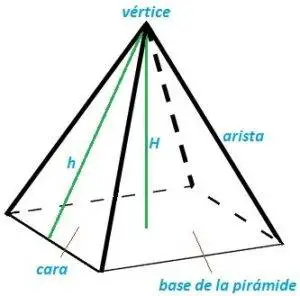
Elementos componentes de toda pirámide:

fig. 5 elementos de la pirámide

H = altura de la pirámide

h = altura del triángulo cara de la pirámide

Volumen de una pirámide:

b = área de la base poligonal de la pirámide

H = altura de la pirámide

Ejemplos:

Pirámide base cuadrada

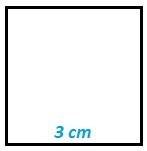fig. 6 base cuadrada de la pirámide

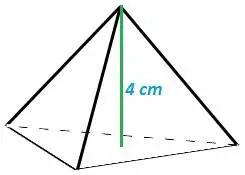
fig. 7 pirámide base cuadrada altura 4 cm

Pirámide base triangular

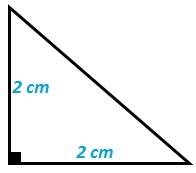fig. 8 base triangular de la pirámide

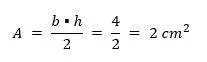fig. 9 pirámide base triangular altura 4 cm

Pirámide base pentagonal cóncava

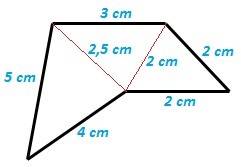fig. 10 base pentagonal cóncava de la pirámide

Para calcular el área de este pentágono irregular cóncavo lo dividimos en tres triángulos, calculamos sus áreas y las sumamos para obtener el área de la base de esta pirámide.

Fórmula de Herón:

Usaremos la fórmula de Herón para calcular el área de estos tres triángulos.

A = área del triángulo abc

s = semi perímetro del triángulo abc

a = valor del lado a del triángulo abc

b = valor del lado b del triángulo abc

c = valor del lado c del triángulo abc

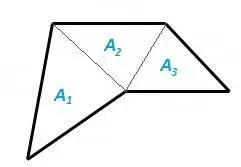fig. 11 áreas de la base pentagonal cóncava de la pirámide

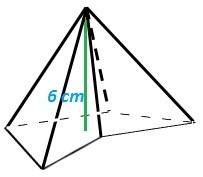fig. 9 pirámide base pentagonal cóncava altura 6 cm

Área de una pirámide:

El área de una pirámide es la suma del área de su base y las áreas de cada una de sus caras.

Ejemplos:

Área del tetraedro

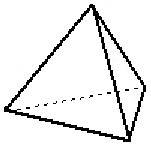fig. 10 pirámide base triangular regular

El tetraedro es un poliedro de forma piramidal compuesto por cuatro triángulos equiláteros.

Por tanto, su área será el área del triángulo equilátero cuadruplicado.

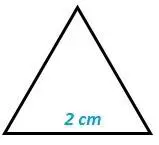fig. 11 triángulo equilátero

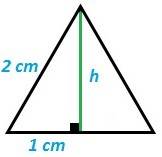fig. 12 área triángulo equilátero

Área de la pirámide base cuadrilátera

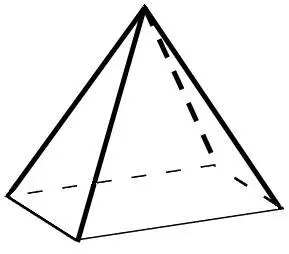fig. 13 pirámide base cuadrilátera

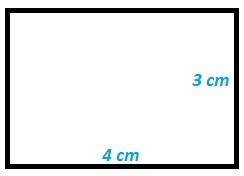fig. 14 área base cuadrilátera

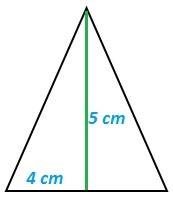
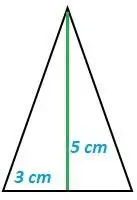
fig. 15 cara 1 de la pirámide de base 4 cm		fig. 16 cara 2 de la pirámide de base 3 cm

Esta pirámide tiene dos caras formadas por triángulos de base 4 cm y dos caras formadas por triángulos de base 3 cm.

Área de la pirámide base pentagonal irregular

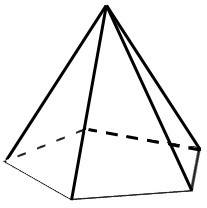fig. 17 pirámide base pentagonal irregular

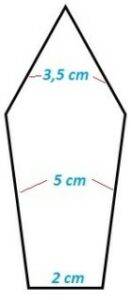fig. 18 área base pentagonal irregular

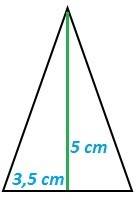
Esta pirámide tiene cinco caras formadas por triángulos de base 2 cm (uno), 3,5 cm (dos) y 5 cm (dos).

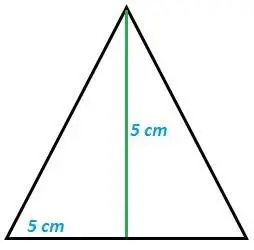
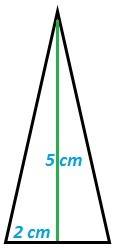
fig. 19 cara 1 de la pirámide de base 5 cm		fig. 20 cara 2 de la pirámide de base 3,5 cm		fig. 21 cara 3 de la pirámide de base 2 cm

Determinante de Gauss

El determinante de Gauss permite calcular el área de cualquier polígono, asignándole coordenadas cartesianas a cada uno de sus vértices y numerándolos en el sentido contrario a las agujas del reloj.

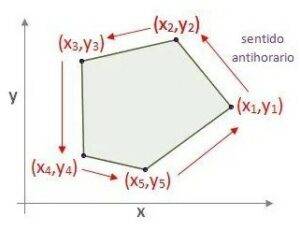fig. 22 numeración de los vértices del polígono

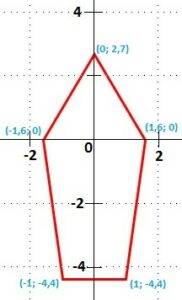fig. 23 coordenadas de los vértices del polígono