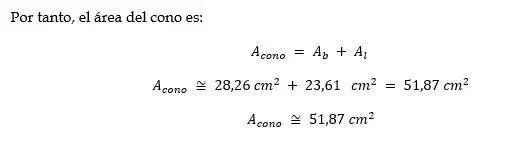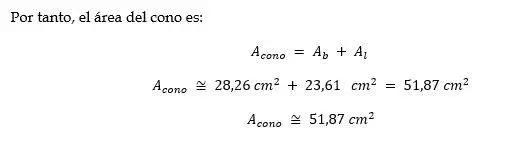Coloquialmente, el área de un cuerpo geométrico es la medida de la superficie que envuelve a dicho cuerpo. En los cuerpos de forma poliédrica, el área es la suma de las áreas de las caras que forman dicho cuerpo.

En los cuerpos redondos y cuerpos de revolución, el área es la suma de la o las bases y/o la transformación, sin deformación, de su superficie redonda en una figura plana.

Áreas de cuerpos geométricos

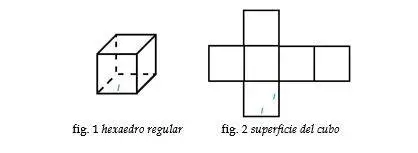
Cubo

Por ser el cubo un cuerpo geométrico con seis caras cuadradas su área es seis veces el área de una de sus caras.

l = valor del lado del cubo

Ejemplo:

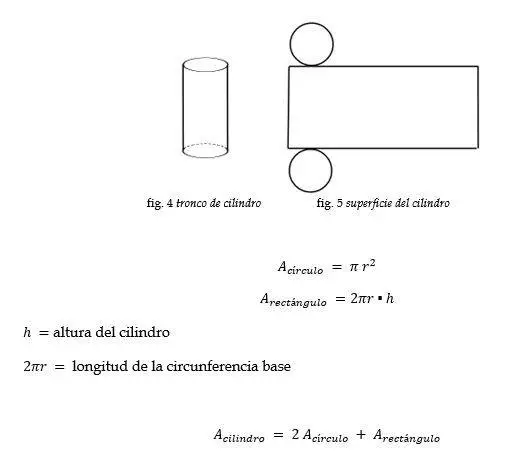
Cilindro

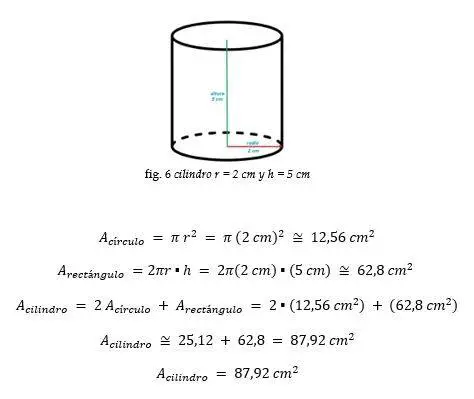
Ejemplo:

Áreas de cuerpos geométricos poliédricos

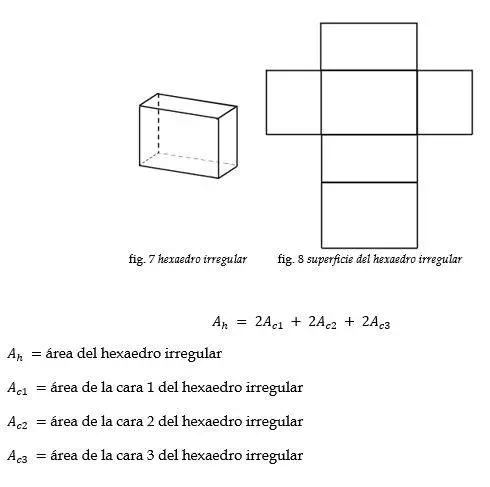
Hexaedro irregular

Ejemplo:

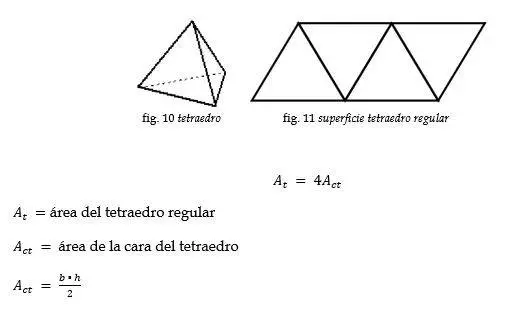
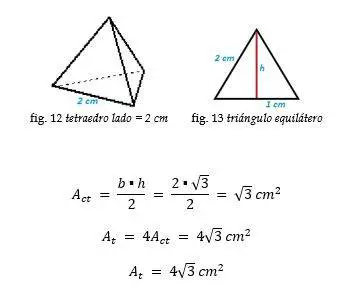
Tetraedro

Ejemplo:

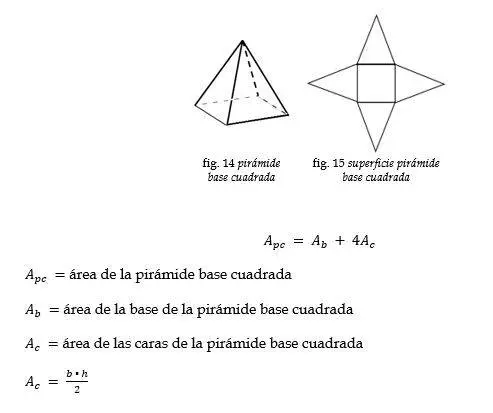
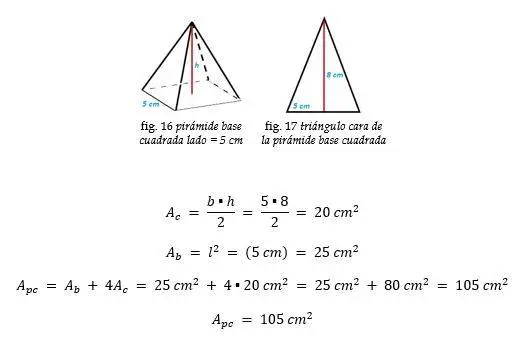
Pirámide base cuadrada

Ejemplo:

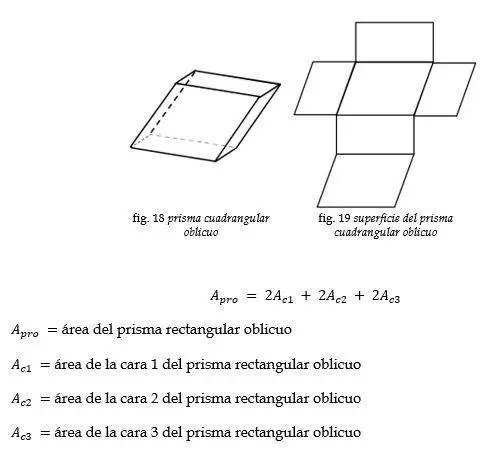
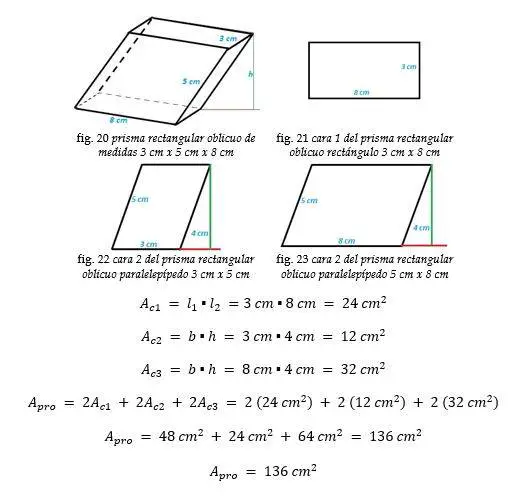
Prisma cuadrangular oblicuo

Ejemplo:

Áreas de cuerpos geométricos redondos

En los cuerpos geométricos redondos analizaremos cómo calcular el área del cono, del cilindro (el cual ya hicimos como ejemplo al comienzo de esta lección) y la esfera, dejaremos al lector los otros cuerpos geométricos redondos que derivan de estos, como el tronco de cono, el tronco de cilindro, el casquete esférico.

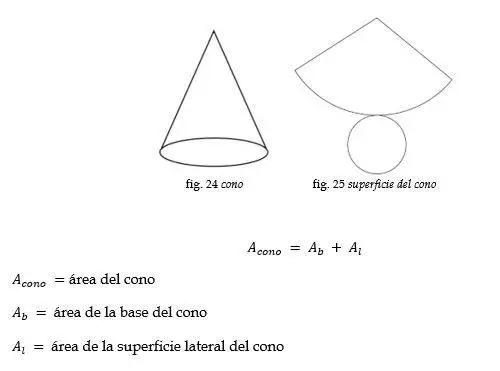
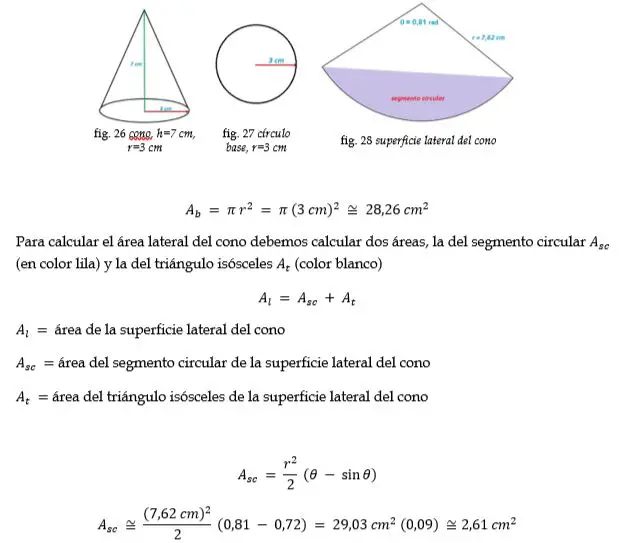
Cono

Ejemplo:

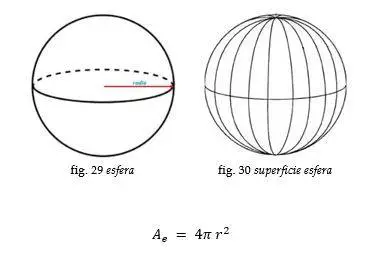
Esfera

Cualquier transformación de la superficie curva de la esfera en una superficie plana conlleva una deformación de dicha superficie. De allí surgen las distintas concepciones de cómo hacer un mapa de la Tierra en el plano.

Las versiones de mapas de la Tierra (proyecciones o transformaciones cartográficas de una esfera en un plano) más conocidas son: La proyección de Gall-Peters o proyección de Peters, la proyección de Mercator y la proyección cilíndrica equivalente.

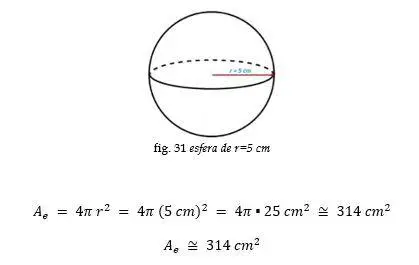
Es por ello que nos limitaremos, por la finalidad de esta lección, a ver un ejemplo de cómo usar la fórmula que nos permite calcular el área de la superficie de una esfera.

Ejemplo:

Áreas de cuerpos geométricos de revolución

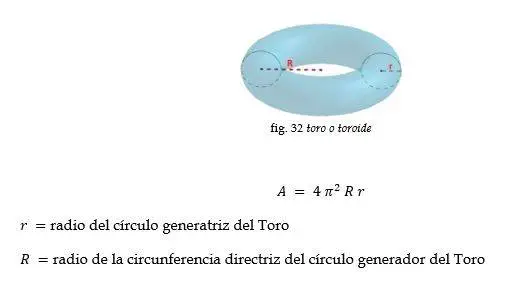
La mayoría de los cuerpos geométricos de revolución requieren para el estudio y cálculo de sus superficies de matemática infinitesimal. Aquí hemos presentado el cálculo de tres superficies de revolución: el tronco de cilindro, el cono y la esfera. Agregaremos el cálculo de la superficie del toro o toroide.

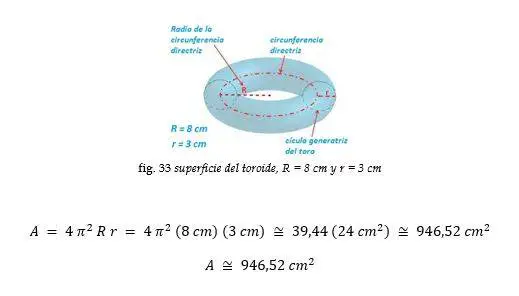
Toro

Ejemplo:

Áreas de cuerpos geométricos compuesto

El desarrollo industrial de máquinas y herramientas llevó al diseño de infinidad de piezas (cuerpos geométricos) que requerían la combinación de varios cuerpos geométricos de distintas especies. Acá ilustraremos con la presentación de dos combinaciones plausibles en el mundo del diseño técnico industrial.

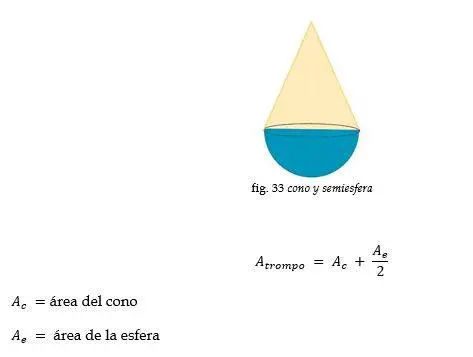
Trompo

Ejemplo:

Perno

Ejemplo: