Ejemplos De Conjugada
Tabla de contenidos
mostrar
Las conjugadas son dos expresiones algebraicas que tienen la misma forma, pero con signos opuestos en uno o varios términos.
- Por ejemplo, las conjugadas del binomio (a + b) son (a – b) y las conjugadas del binomio (2x + 3y) son (2x – 3y).
Las conjugadas son importantes en diversas ramas de las matemáticas, como el álgebra, el cálculo y la teoría de números. En el álgebra, por ejemplo, se utilizan las conjugadas para simplificar expresiones, factorizar polinomios y encontrar raíces de ecuaciones. En el cálculo, las conjugadas se utilizan para racionalizar expresiones y simplificar cálculos.
Ejemplos de denominación de conjugada
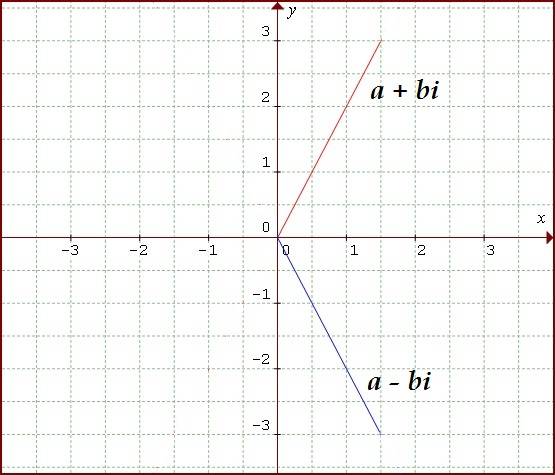
$$Sea\;Z=a+bi\;un\;número\;complejo,\;\overline Z=a-bi\;es\;la\;conjugada\;de\;Z$$
$$Sea\;(a+\sqrt b)\;un\;binomio\;irracional,\;Su\;conjugada\;es\;el\;binomio\;(a-\sqrt b)$$
Ejemplos de conjugadas
| $$(3+\sqrt{\frac12})$$ | $$Z=\sqrt5-3i$$ | $$(x-\sqrt{5y})$$ | $$Z=3i+4$$ |
| $$(\sqrt6+\sqrt{\frac38})$$ | $$Z=\sqrt{18}-7i$$ | $$a\sqrt{b-\sqrt{5ab}}$$ | $$Z=1+\sqrt{\frac12i}$$ |
| $$1-\sqrt7$$ | $$Z=3-i$$ | $$(\sqrt6+6)$$ | $$Z=4i$$ |
| $$(2a-\sqrt{10})$$ | $$Z=\frac13+2i$$ | $$\sqrt{22}+\sqrt{11}$$ | $$Z=15-5i$$ |
| $$(\frac6{32}-\sqrt2)$$ | $$Z=2+i$$ | $$(6n+\sqrt{5n^3})$$ | $$(2\sqrt x-\sqrt{3x})$$ |
| $$Z=11-11i$$ | $$Z=\frac12+\frac13i$$ | $$(3+\sqrt3)$$ | $$Z=\frac18-13i$$ |
Ejemplos resueltos de conjugadas
$$Z=3+i\;\Rightarrow\overset{}Z=3-i$$
$$(6-\sqrt7)\Rightarrow(6+\sqrt7)$$
$$Z=\sqrt3-7i\;\Rightarrow\overset{}Z=\sqrt3+7i$$
$$(\sqrt3+\sqrt2)\Rightarrow(\sqrt3-\sqrt2)$$
Representación gráfica de un número complejo y su conjugada
Usos más frecuentes de las conjugadas
-
- En el caso de los números complejos, cuando dividimos por un numero complejo la conjugada se usa para convertir el denominador en un número real (como cuando se racionaliza el denominador).
- Cuando se multiplica un número imaginario por su conjugado obtenemos un número real. El siguiente es un ejemplo de este caso:
$$(4+3i)\times(4-3i)=16-12i+12i-9i^2=16-9(-1)=16+9=25$$
- En el caso de los radicales en forma de binomio, cuando en una división el denominador es un binomio con uno o dos números irracionales, se convierte el denominador en un número real al multiplicarlo por su conjugada.
- Cuando se multiplica un radical en forma de binomio por su conjugada obtenemos un número real. Ejemplo de esto sería:
$$(1+\sqrt2)\times(1-\sqrt2)=\;1-\sqrt2+\sqrt2-(\sqrt2\times\sqrt2)=1-\sqrt4=1-2=-1$$
¿Te ha gustado lo que has leído?
¡Gracias por tu votación!
Artículos recomendados
Ejemplos de microrrelatos
Ejemplos De Gentilicios
Anorexia: Características, Síntomas, Riesgos, Prevención Y Más
Páginas Más Interesantes De Internet Para Ver Películas Legalmente
Ejemplos de Comunicación Interna
Ejemplos de Metáforas de Amor
10 Ejemplos De Psicoterapia Que Debes Conocer
50 Ejemplos de Fortalezas y Debilidades de una Persona
Ejemplos De Países Y Capitales De Asia Oriental
Características de la personalidad
10 Ejemplos De Agresividad – Características Causas Y Cómo Evitarla
¿Te ha gustado lo que has leído?
¡Gracias por tu votación!