Ejemplos De Derivadas
Las derivadas son una herramienta matemática que nos permite encontrar la tasa de cambio instantánea de una función en un punto dado. En otras palabras, nos permite encontrar la pendiente de una curva en un punto específico.
- Por ejemplo, si tenemos una función f(x) = x2, la derivada de esta función nos dará la tasa de cambio instantánea de la función en cualquier punto de la curva. La derivada de la función f(x) se denota como f'(x) o dy/dx.
La fórmula para calcular la derivada de una función es:
f'(x) = lim (h->0) [f(x+h) – f(x)] / h
Esto significa que tomamos el límite de la diferencia de la función evaluada en dos puntos muy cercanos, dividida por la distancia entre esos puntos, cuando la distancia entre los dos puntos se acerca a cero.
- Por ejemplo, si queremos encontrar la derivada de la función f(x) = x2 en el punto x = 3, podemos utilizar la fórmula de la derivada:
f'(x) = lim (h->0) [f(x+h) – f(x)] / h
f'(3) = lim (h->0) [(3+h)2 – 32] / h
f'(3) = lim (h->0) [9 + 6h + h2 – 9] / h
f'(3) = lim (h->0) (6h + h2) / h
f'(3) = lim (h->0) (6 + h)
f'(3) = 6
Por lo tanto, la derivada de la función f(x) = x2 en el punto x = 3 es igual a 6. Esto significa que la pendiente de la curva de la función en el punto x = 3 es igual a 6.
Las derivadas se utilizan en muchas áreas de la ciencia y la ingeniería para modelar el cambio y el movimiento. Además, la derivada de una función puede ser utilizada para encontrar los puntos máximos y mínimos de la función, lo que es útil para la optimización y la resolución de problemas.
Explicación sencilla
Las derivadas son una herramienta fundamental en el cálculo y la matemática en general. En términos simples, la derivada de una función describe cómo cambia la función en un punto específico. Esto es útil para entender cómo se comportan las funciones y para resolver problemas en física, economía, ingeniería y muchas otras áreas.
Para calcular la derivada de una función, se utiliza la regla de la derivada, que es un conjunto de fórmulas que describen cómo se comportan diferentes tipos de funciones.
- Un ejemplo práctico de la utilidad de las derivadas es en la física, donde se utilizan para calcular la velocidad y la aceleración de un objeto en movimiento. Si se conoce la posición de un objeto en función del tiempo, se puede calcular su velocidad como la derivada de la función de posición con respecto al tiempo. De manera similar, la aceleración se puede calcular como la derivada de la velocidad con respecto al tiempo.
Puedes descargar un documento con estas reglas básicas en el siguiente enlace: Reglas Basicas para Derivar
Ejemplo de Derivadas
| $$f(x)=x^3+2x^2-5x+1\;\Rightarrow\;f'(x)=3x^2+4x-5$$ |
| $$f(x)=(2x+1)(3x-4)\;\Rightarrow\;f'(x)=6x-5$$ |
| $$f(x) = e^x cos(x) f'(x) = e^x cos(x) – e^x sin(x)$$ |
| $$f(x)\;=\;\ln(2x\;+\;1)\;\;\Rightarrow\;f'(x)\;=\;2/(2x\;+\;1)$$ |
| $$f(x)=sin^2(x)+cos^2(x)\;\Rightarrow f'(x)=0$$ |
| $$f(x)=\sqrt{(x^3-1)};\Rightarrow\;f'(x)=(3x^2)/(2\sqrt{(x^3-1)})$$ |
| $$f(x)=(x^2+3x-1)/(2x-3)\;\Rightarrow\;f'(x)=(4x+3)/((2x-3)^2)$$ |
| $$f(x)=e^(2x)+3x^2\;\Rightarrow\;f'(x)=2e^(2x)+6x$$ |
| $$f(x)=(3x^2-1)/(x^3+2x+1)\;\Rightarrow\;f'(x)=(-3x^4-4x^2+6x+2)/((x^3+2x+1)^2)$$ |
Puedes descargar un documento con 100 ejemplos mas de derivadas en el siguiente enlace: Ejemplos de Derivadas
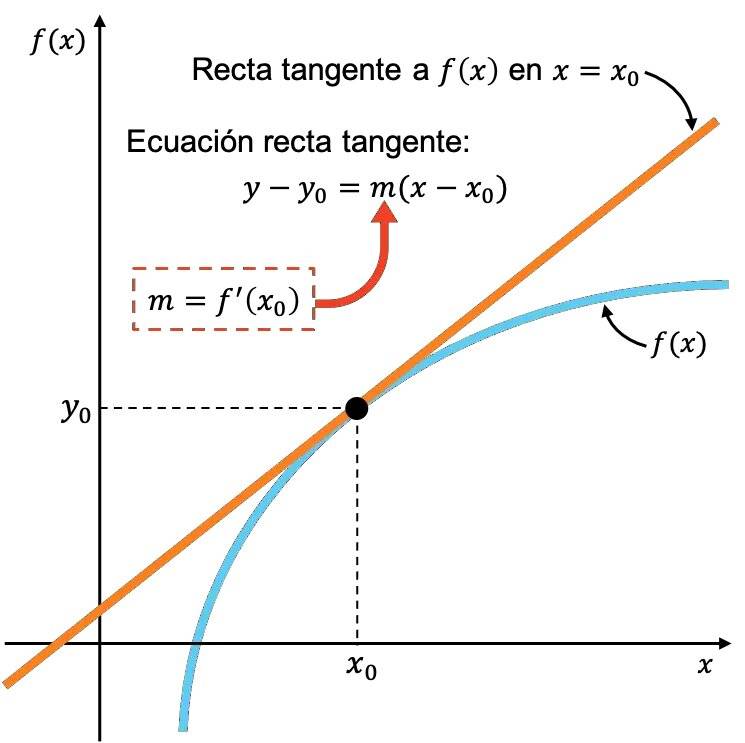
La derivada de una función
La ecuación de la recta tangente a la gráfica y=g(x) que pasa por el punto (x0, y0) es:
$$y-y_0=g'(x_0)(x-x_0)$$
Una función nos indica los cambios de un fenómeno dado que queda plasmado en una gráfica, reflejando la transformación que le ocurre a una variable independiente a través de dicha función.
La derivada de esa función nos indica cómo es la velocidad de esos cambios en cada uno de los puntos de la gráfica de la función.
Propiedades de la Derivada
Las propiedades de las derivadas son reglas matemáticas que describen cómo se comportan las derivadas de diferentes tipos de funciones. Estas propiedades son muy útiles para simplificar y acelerar los cálculos de derivadas, y también son importantes para entender mejor cómo funcionan las funciones y cómo se relacionan entre sí.
Las siguientes son sólo algunas de las propiedades más comunes de las derivadas:
Linealidad: La derivada de la suma (o la diferencia) de dos funciones es igual a la suma (o la diferencia) de las derivadas de esas funciones. En otras palabras, si f(x) y g(x) son dos funciones, entonces
$$(f(x)\;+\;g(x))’\;=\;f'(x)\;+\;g'(x)\;y\;(f(x)\;-\;g(x))’\;=\;f'(x)\;-\;g'(x)$$
Regla del producto: La derivada del producto de dos funciones f(x) y g(x) es igual a f'(x)g(x) + f(x)g'(x). En otras palabras, si h(x) = f(x)g(x), entonces
$$h'(x)\;=\;f'(x)g(x)\;+\;f(x)g'(x)$$
Regla de la cadena: La derivada de la composición de dos funciones h(x) = f(g(x)) es igual al producto de la derivada de la función exterior f'(u) evaluada en la función interior g(x), y la derivada de la función interior g'(x). En otras palabras
$$h'(x)\;=\;f'(g(x))g'(x)$$
Regla del cambio de variable: Si y = f(u) y u = g(x), entonces
$$\frac{dy}{dx}\;=\;\frac{dy}{du}\;\times\;\frac{du}{dx}$$
Esta última regla es útil para calcular derivadas de funciones que involucran una variable intermedia.