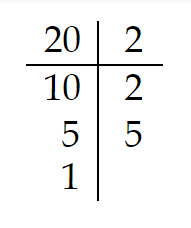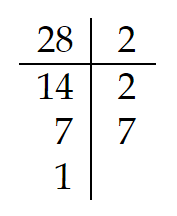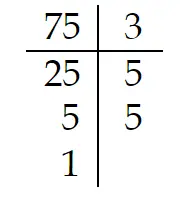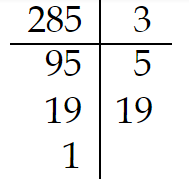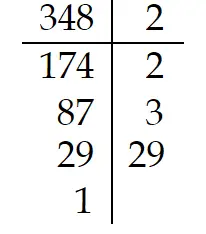Ejemplos de Divisores

Los Divisores de un número entero diferente de cero son los números que lo dividen de manera exacta, es decir, con residuo cero. Acá te mostraremos cómo calcularlos y algunos Ejemplos de Divisores.

¿Todos los números enteros diferentes de cero tienen divisores?

Sí, aunque para algunos casos resulte evidente.

Ejemplo

El número 2 tiene dos divisores, el número 1 y él mismo

div (2) = (1, 2)

¿Existen varios tipos de divisores?

Algunos autores los clasifican en dos tipos, los divisores propios y los divisores impropios.

Los divisores impropios son el número 1 que es divisor de todos los números enteros diferentes de cero y el mismo número al que se le desea calcular sus divisores.

Así tenemos que para todo número n con n ≠ 0 sus divisores impropios serán el número 1 y el número n

Los divisores propios son todos aquellos números que dividen de manera exacta al número entero y son distintos del número 1 y de sí mismo.

Así tenemos que los divisores propios del número 8 son el número 2 y el 4

¿Cómo calcular los divisores de un número entero cualquiera?

1. La forma más simple es la que se desprende de su definición, si te piden calcular los divisores de un número entero cualquiera diferente de cero comienzas a dividirlo entre 2, 3, 4, 5, 6… y todas las divisiones que te den residuo cero te da un divisor.
2. Esta tarea para muchos números es titánica, por ello, otra forma para calcular los divisores de número entero diferente de cero es usando la descomposición en sus factores primos.

Ejemplos ilustrativos:

1. Calculemos los divisores del número 30

Divisores impropios de 30 son 1, 30

Divisores propios los que aparecen en la columna de la derecha y todas las multiplicaciones distintas posibles entre ellos 2, 3, 5, 2 x 3, 2 x 5, 3 x 5, es decir: 2, 3, 5, 6, 10, 15

Por tanto, div (30)= (1, 2, 3, 5, 6, 10, 15, 30)

1. Calculemos los divisores del número 54

Divisores impropios de 54 son 1, 54

Divisores propios los que aparecen en la columna de la derecha y todas las multiplicaciones distintas posibles entre ellos 2, 3, 2 x 3, 3 x 3, 2 x 3 x 3, 3 x 3 x 3, es decir: 2, 3, 6, 9, 18, 27

Por tanto, div (54)= (1, 2, 3, 6, 9, 18, 27, 54)

3. Casos especiales en el cálculo de divisores
4. Divisores de un número es primo son el número 1 y él mismo
5. Divisores de una potencia de un número primo

Si el número es pⁿ con p primo y n natural distinto de cero, sus divisores serán los divisores impropios y el número primo elevado a 1, 2…, n-1.

Es decir div (pⁿ) = 1, p, p², p³,…, pⁿ

Ejemplo:

32 = 2⁵

Por tanto, div (32)= 1, 2, 2², 2³, 2⁴, 2⁵, es decir: div (32)= (1, 2, 4, 8, 16, 32)

Ejemplos

• ¿Cuáles son los divisores de 20?

Todas las multiplicaciones distintas posibles de los números de la columna de la derecha

div (20)= (1; 2, 5; 2×2, 2×5; 2x2x5)

Calculamos:

div (20)= (1; 2, 5; 4, 10; 20)

Ordenamos:

div (20)= (1, 2, 4, 5, 10, 20)

 

• ¿Cuáles son los divisores de 28?

div (28)= (1; 2, 7; 2×2, 2×7; 2x2x7)Todas las multiplicaciones distintas posibles de los números de la columna de la derecha

Calculamos:

div (28)= (1; 2, 7; 4, 14; 28)

Ordenamos:

div (28)= (1, 2, 4, 7, 14, 28)

 

• ¿Cuáles son los divisores de 75?

Todas las multiplicaciones distintas posibles de los números de la columna de la derecha

div (75)= (1; 3, 5; 3×5, 5×5; 3x5x5)

Calculamos:

div (75)= (1, 3, 5, 15, 25, 75)

 

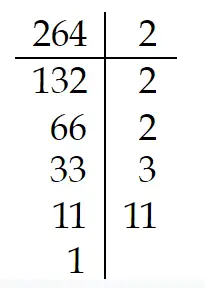
• ¿Cuáles son los divisores de 264?

Para calcular todos los divisores propios, adicionales a los que aparecen en la columna de la derecha (2, 2, 3, 11) vamos a hallar todas las multiplicaciones distintas posibles de todos los números que aparecen en esa columna

Veamos las multiplicaciones distintas posibles de dos números:

(2×2); (2×3); (2×11); (3×11)

De tres números:

(2x2x2); (2x2x3); (2x2x11); (2x3x11)

De cuatro números:

(2x2x2x3), (2x2x2x11); (2x2x3x11)

Por tanto:

div (264)=    (1; 2, 3, 11; 2×2, 2×3, 2×11, 3×11; 2x2x2, 2x2x3, 2x2x11, 2x3x11; 2x2x2x3, 2x2x2x11, 2x2x3x11; 2x2x2x3x11)

Calculamos:

div (264)= (1; 2, 3, 11; 4, 6, 22, 33; 8, 12, 44, 66; 24, 88, 132; 264)

Ordenamos:

div (264)= (1, 2, 3, 4, 6, 8, 11, 12, 22, 24, 33, 44, 66, 88, 132, 264)

 

• ¿Cuáles son los divisores de 285?

div (285)= (1; 3, 5, 19; 3×5, 3×19, 5×19; 3x5x19)Todas las multiplicaciones distintas posibles de los números de la columna de la derecha

Calculamos:

div (285)= (1; 3, 5, 19; 15, 57, 95; 285)

Ordenamos:

div (285)= (1, 3, 5, 15, 19, 57, 95, 285)

 

• ¿Cuáles son los divisores de 348?

2, 3, 9 Veamos todos los divisores propios de 348

Adicionalmente, todas las multiplicaciones distintas posibles de los números que aparecen en la columna derecha de la descomposición en factores primos

(2×2); (2×3); (2×29); (3×29)

(2x2x3); (2x2x29); (2x3x29)

Entonces:

div (348)= (1; 2, 3, 29; 2×2, 2×3, 2×29, 3×29; 2x2x3, 2x2x29, 2x3x29; 2x2x3x29)

Calculamos:

div (348)= (1; 2, 3, 29; 4, 6, 58, 87; 12, 116, 174; 348)

Ordenamos:

div (348)= (1, 2, 3, 4, 6, 12, 29, 58, 87, 116, 174, 348)

 

• ¿Cuáles son los divisores de 6930?

div (6930)=  (1; 2, 3, 5, 7, 11; 2×3, 2×5, 2×7, 2×11, 3×3, 3×5, 3×7, 3×11, 5×7, 5×11, 7×11; 2x3x3, 2x3x5, 2x3x7, 2x3x11, 2x5x7, 2x5x11, 2x7x11, 3x3x5, 3x3x7, 3x3x11, 3x5x7, 3x5x11, 3x7x11, 5x7x11; 2x3x3x5, 2x3x3x7, 2x3x3x11, 2x3x5x7, 2x3x5x11, 2x3x7x11, 2x5x7x11, 3x3x5x7, 3x3x5x11, 3x3x7x11, 3x5x7x11; 2x3x3x5x7, 2x3x3x5x11, 2x3x3x7x11, 2x3x5x7x11, 3x3x5x7x11; 2x3x3x5x7x11)

Calculamos:

div (6930)=  (1; 2, 3, 5, 7, 11; 6, 10, 14, 22, 9, 15, 21, 33, 35, 55, 77; 18, 30, 42, 66, 70, 110, 154, 45, 63, 99, 105, 165, 231, 385; 90, 126, 198, 210, 330, 462, 770, 315, 495, 693, 1155; 630, 990, 1386, 2310, 3465; 6930)

Ordenamos:

div (6930)=   (1, 2, 3, 5, 6, 7, 9, 10, 11, 14, 15, 18, 21, 22, 30, 33, 35, 42, 45, 55, 63, 66, 70, 77, 90, 99, 105, 110, 126, 154, 165, 198, 210, 231, 315, 330, 385, 462, 495, 630, 693, 770, 990, 1155, 1386, 2310, 3465, 6930)

 

El artículo ha sido realizado por el profesor Licenciado en Matemáticas: Ángel Míguez Álvarez