Los números complejos constituyen un cuerpo algebraico de elementos de la forma a + i ▪ b, donde a representa la parte real y b la parte imaginaria.
Ejemplos de números complejos
Históricamente los números complejos se relacionaron con la existencia de una fórmula analítica (como la conocida para las ecuaciones de segundo grado) para hallar las raíces de una ecuación cúbica.
Ejemplo:
- x³ = 9 ▪ x + 28
Hacemos uso de (C) para hallar una raíz de esta ecuación cúbica
Por simple sustitución se puede comprobar el resultado obtenido.
Sin embargo, hay casos donde por este método no se obtiene una solución real a la ecuación cúbica.
Ejemplo:
Las ecuaciones cúbicas pueden tener tres posibles tipos de soluciones:
- Tres raíces reales, donde al menos dos de ellas son idénticas,
- Una raíz real y dos raíces imaginarias y
- Tres raíces reales distintas
Estos casos, pese a todos los desarrollos realizados durante 3 siglos, llevaban a que la existencia de los números imaginarios generara dudas entre los matemáticos.
Fueros los aportes de Carlos Federico Gauss, durante el siglo XIX, que al darle una representación gráfica a los números complejos disipó las dudas existentes.
Números complejos como extensión de los números reales
En el sistema escolar se enseñan los conjuntos numéricos extendiendo el conjunto numérico ya estudiado de forma que permita hallar la solución que el sistema anterior no permitía resolver.
Ejemplos:
Pues bien, se puede afirmar que la existencia de los números imaginarios nace como la solución a la ecuación:
Representación geométrica de los números complejos
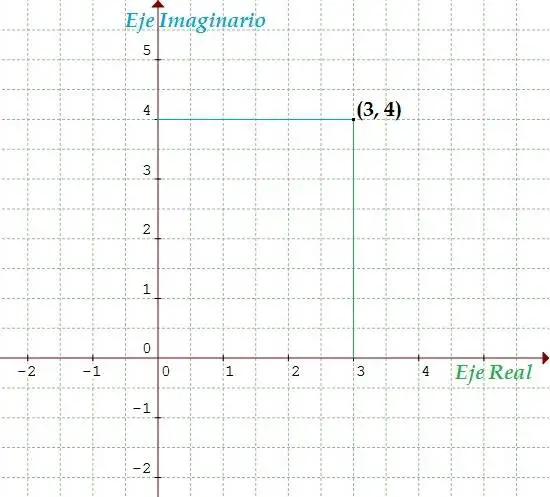
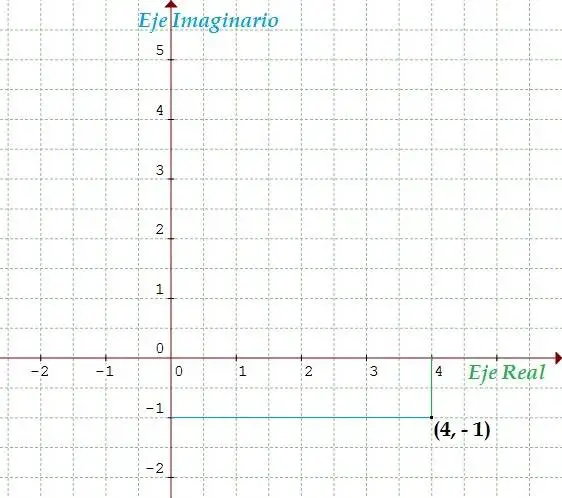
Los números complejos, a propuesta de Gauss, se representaban como un par ordenado donde a representa el componente real y b el componente imaginario. Se representaban como un punto en el plano.
Ejemplos:
- (3, 4) parte real = 3 parte imaginaria = 4
- (4, – 1) parte real = 4 parte imaginaria = – 1
Representación Vectorial de los números complejos
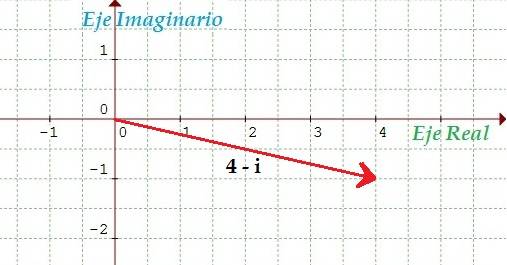
Los números complejos no son números en el sentido conocido por todos los que han transitado por el sistema escolar, no se usan para cálculos y mediciones, representan objetos matemáticos que pueden asemejarse al que se le da a los vectores en el plano.
Ejemplos:
- 3 + 4i parte real = 3 parte imaginaria = 4
- 4 – i parte real = 4 parte imaginaria = – 1
En muchos libros de texto de matemáticas suele designarse la letra z para denominar los números complejos.
Representación trigonométrica de los números complejos
Usando las razones trigonométricas tenemos que:
Ejemplos:
Pues bien, a partir del siglo XIX se comenzó a develar el misterio de los números complejos, sus formas de representación allanaron el camino para la realización de operaciones con ellos, similares a las conocidas con pares ordenados, con vectores, es decir, adición, sustracción, multiplicación y división.
Y con la fórmula de Moivre la forma trigonométrica develó como hallar la potenciación y la radicación. También con esto sus aplicaciones en diversas ramas de las ciencias y las tecnologías.
Ángel Míguez Álvarez
