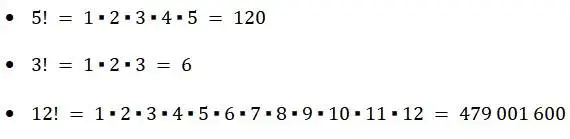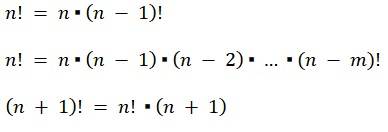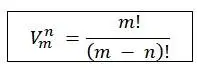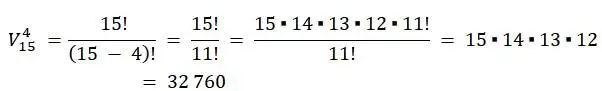Las permutaciones, variaciones y combinaciones de elementos o números nos permiten determinar cuáles elementos pertenecen a un conjunto cualquiera con base en sus características que lo definen.

Contar es una actividad primigenia del ser humano, desde el uso de los palotes para saber cuántos somos o cuánto tengo.

A medida que fue creciendo la población, con la creación de los procesos de producción a gran escala, se fue complejizando las necesidades de contar, de ahí la creación de la teoría combinatoria que nos permite contar conjuntos finitos e infinitos de distintas maneras con base en sus características.

Combinatoria

La Teoría Combinatoria es parte del Análisis que investiga el número de posibilidades de la ordenación, selección e intercambio de los elementos de un conjunto.[1]

La herramienta clave para estos conteos complejos y sus distintas formas de ordenación es el factorial de un número.

Factorial de un Número

Es una forma algebraica de presentar el producto de una cantidad determinada de números naturales.

Ejemplos:

Se considera que:

Adicionalmente

Permutaciones (o Permutaciones sin repetición)

De los elementos de un conjunto es una forma de colocar los mismos en un orden determinado, son formas de agrupar dichos elementos de manera que:

1. Se consideran todos los elementos del conjunto.
2. No se repiten ningún elemento del conjunto.
3. El orden en el que se agrupan dichos elementos es considerado para su diferenciación.

Ejemplo:

• ¿Cuántos números naturales distintos se pueden crear con cuatro dígitos distintos no nulos?

Tenemos: {3, 5, 6, 8}

Podemos crear los siguientes números 3568, 3586, 3658. 3685, 3856, 3865, 5368, 5386, 5836, 5863, 5638, 5683, 6358, 6385, 6835, 6853, 6583, 6538, 8356, 8365, 8635, 8653, 8563, 8536.

Podemos crear 24 números distintos.

Fórmula:

Ejemplo:

• ¿De cuántas maneras distintas puedo colocar en mi llavero, las 5 llaves que uso a diario?

Por tanto, las puedo colocar de 120 maneras distintas. ¿Será por eso que todos las ponemos en un orden de uso cotidiano?

Variaciones (o Variaciones sin Repetición)

Son permutaciones de una selección de n de elementos de un conjunto de m elementos. Esta es otra forma de agrupar elementos de manera que:

1. Se toman solo algunos elementos del conjunto.
2. No se repite ningún elemento del conjunto.
3. El orden en el que se agrupan dichos elementos es considerado para su diferenciación, , es decir el binomio (a, b) ≠ (b, a)

Ejemplo:

• ¿Cuántas banderas de dos franjas verticales de colores distintos se pueden crear con 6 retazos de tela de colores distintos?

Tenemos:  = {Azul, Verde, Rojo, Amarillo, Naranja, Violeta} {Az, Ve, R, Am, N, Vi}.

Podemos formar las siguientes Banderas: (Az, Ve); (Az, R); (Az, Am); (Az, N); (Az, Vi); (Ve, Az); (Ve, R); (Ve, Am); (Ve, N); (Ve, Vi); (R, Az); (R, Ve); (R, Am); (R, N); (R, Vi); (Am, Az); (Am, Ve); (Am, R); (Am, N); (Am, Vi); (N, Az); (N, Ve); (N, R); (N, Am); (N, Vi); (Vi, Az); (Vi, Ve); (Vi, R); (Vi, Am); (Vi, N).

Podemos formar 30 banderas distintas de dos franjas verticales.

Fórmula:

Ejemplo:

• En un torneo de damas chinas en el que participan 15 estudiantes de una escuela se premiarán el primer lugar, el segundo lugar y dos en el tercer lugar. ¿De cuántas maneras distintas se podrá presentar el cuadro ganador?

Por tanto, el cuadro ganador se puede presentar de 32 760 maneras distintas, es por ello que nadie lo conforma hasta terminado el torneo.

Combinaciones (o Combinaciones sin repetición)

Son formas de agrupar elementos de un conjunto en las que:

1. Se toman solo algunos elementos del conjunto.
2. No se repite ningún elemento del conjunto.
3. El orden en el que se agrupan dichos elementos no es tomado en cuenta, es decir el binomio (a, b) = (b, a).

Ejemplo:

• ¿De cuántos colores distintos puedo hacer gelatinas para una fiesta infantil si cuento solo con cuatro colores distintos?

Tenemos: (Verde Limón, Naranja, Rojo Fresa, Violeta Mora) = (Ve, N, R, Vi)

Podemos hacer estas gelatinas de colores diferentes: (Ve, N); (Ve, R); (Ve, Vi); (N, R); (N, Vi); (R, Vi)

Podemos generar seis colores distintos de gelatinas.

Fórmula:

Ejemplo:

• Necesitamos pintar un gran galpón y para hacerlo debemos comprar tres potes de pintura con el fin de cubrir todas las paredes, en la tienda de pintura han tenido problemas con su proveedor y solo le quedan siete potes de pintura de diferentes colores. Si no nos importa de qué color quedan pintadas las paredes del galpón ¿Cuántas mezclas distintas podemos hacer?

Por tanto, puedo hacer 70 combinaciones distintas de colores con los potes disponibles y la necesidad para cubrir las paredes del galpón.

Ejercicios:

1. ¿Cuántos números de 6 cifras diferentes se puede formar con los dígitos: 2, 4, 6, 3, 5, 9?
2. Si en el aula laboratorio hay 8 puestos de trabajo, ¿de cuántas maneras distintas se pueden sentar los estudiantes en los puestos de trabajo?
3. Si la mesa de mi comedor es de cuatro puestos, ¿de cuántas formas distintas nos podemos sentar mis tres invitados y yo alrededor de ella?
4. ¿Cuántos números de 5 cifras se pueden formar usando solo dígitos impares?
5. ¿Cuántos números distintos de tres cifras diferentes se pueden escribir con los dígitos pares sin el cero?
6. En un salón de clase hay 24 estudiantes. ¿De cuántas formas distintas se puede escoger un equipo de baloncesto?
7. En una final de atletismo, con siete competidores, ¿de cuántas formas distintas se puede conformar el podio ganador?
8. Una mamá va a preparar una ensalada para su familia y dispone de célery, zanahoria, ají dulce y lechuga. ¿De cuántas formas se puede preparar la ensalada usando solo dos ingredientes?
9. Se va a programar un torneo de dominó para los diez integrantes de un equipo de la urbanización. ¿Cuántos partidos se deben programar si cada participante jugará con cada uno de los demás miembros del equipo?

Las permutaciones, variaciones y combinaciones se usan en la estadística, álgebra, física y teoría de juegos, entre otras.

Ángel Míguez Álvarez

[1] Ströbl, W. (1 977). Diccionarios Rioduero Matemática. España, Madrid: Ed. Rioduero p. 49