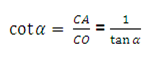20 Ejemplos De Razones Trigonométricas
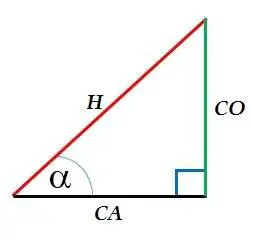
Las razones trigonométricas son los cocientes o razones que se establecen entre los catetos y la hipotenusa de un triángulo rectángulo con base en los valores de sus ángulos internos.
Ejemplo de razones trigonométricas
Círculo Trigonométrico
El círculo trigonométrico es un círculo con centro en el origen del plano cartesiano de radio 1 en el que se establecen las relaciones y valores trigonométricos del radio vector unitario cuando gira con un ángulo determinado dentro del círculo trigonométrico.
Ejemplos:
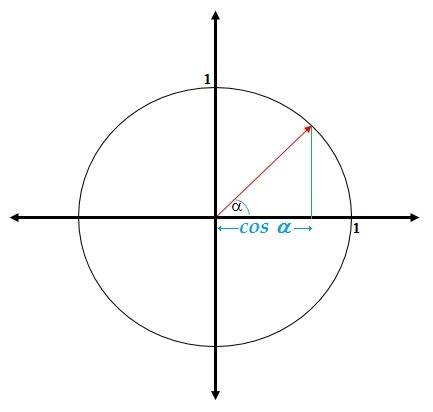
- Se define el coseno del ángulo a en el plano cartesiano, como la proyección ortogonal sobre el eje x del radio vector cuando ha girado en el sentido contrario a las agujas del reloj un ángulo α.
Se entenderá la proyección ortogonal sobre el eje x, la sombra del radio vector sobre el eje x.
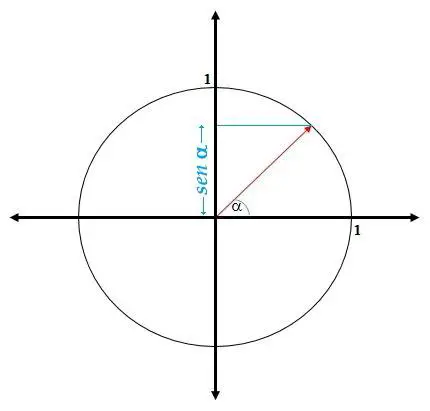
- Se define el seno del ángulo a en el plano cartesiano como la proyección ortogonal sobre el eje y, del radio vector cuando ha girado en el sentido contrario a las agujas del reloj un ángulo α.
Se entenderá la proyección ortogonal sobre el eje y, la sombra del radio vector sobre el eje y.
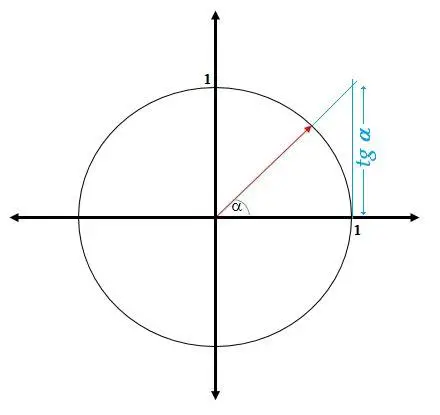
- Se define la tangente del ángulo a en el plano cartesiano como la intercepción del radio vector cuando ha girado en el sentido contrario a las agujas del reloj un ángulo a con la recta tangente al círculo trigonométrico en el punto (1, 0) del plano cartesiano.
Otras razones trigonométricas
Cotangente
La cotangente del ángulo a es la razón entre el Cateto Adyacente y el Cateto Opuesto, es decir la inversa de la tangente del ángulo α
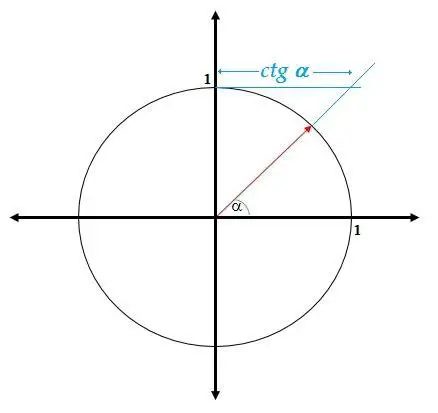
O también la podemos definir como como la intercepción del radio vector cuando ha girado en el sentido contrario a las agujas del reloj un ángulo a con la recta tangente al círculo trigonométrico en el punto (0, 1) del plano cartesiano.
Secante
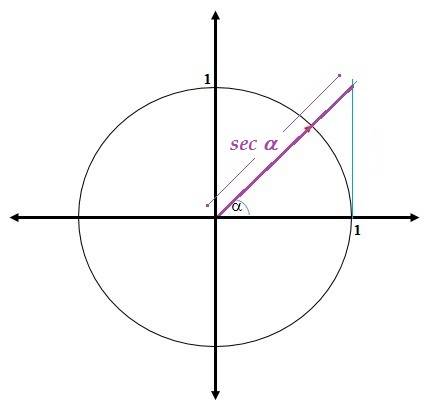
La secante del ángulo a es la razón entre el Hipotenusa y el Cateto Adyacente, es decir la inversa del coseno del ángulo α
También puede ser definida como la prolongación del radio vector hasta interceptar la tangente del ángulo α
Cosecante
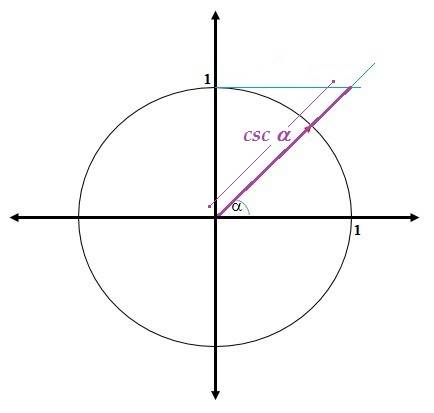
La cosecante del ángulo a es la razón entre el Hipotenusa y el Cateto Opuesto, es decir la inversa del seno del ángulo α
También puede ser definida como la prolongación del radio vector hasta interceptar la cotangente del ángulo α.
Ejercicios de razones trigonométricas
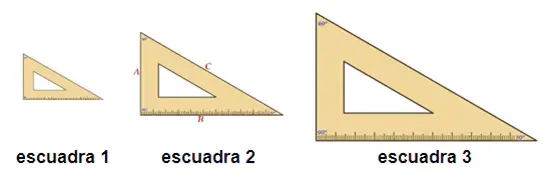
Tome dos o tres escuadras escalena (cartabón) de distintos tamaños y dimensiones.
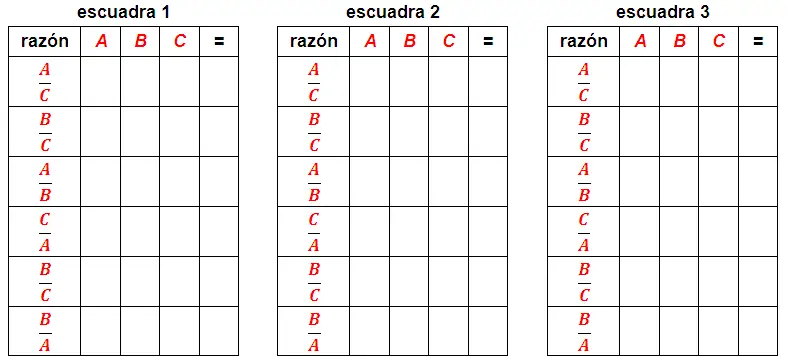
Efectúe las razones indicadas y con esos datos rellene las siguientes tablas para cada uno de las escuadras medidas:
- Con base en los datos obtenidos determine el significado de cada razón (¿seno, coseno, tangente, cosecante, secante y cotangente?) respecto al ángulo de 30° y luego con respecto al ángulos de 60°
- ¿De qué dependen los valores obtenidos, del tamaño de la escuadra o del ángulo?
- Dibuje el ángulo de 60° y determine el valor del coseno usando una regla milimetrada
- Dibuje el ángulo de 30° y determine el valor del seno usando una regla milimetrada
- Dibuje el ángulo de 45° y determine el valor de la tangente usando una regla milimetrada
- Dibuje el ángulo de 90° y determine el valor del coseno usando una regla milimetrada
- Dibuje el ángulo de 150° y determine el valor del seno usando una regla milimetrada
- Dibuje el ángulo de 135° y determine el valor de la tangente usando una regla milimetrada
- Dibuje el ángulo de 180° y determine el valor del seno usando una regla milimetrada
- Dibuje el ángulo de 270° y determine el valor del seno usando una regla milimetrada
- Dibuje el ángulo de 360° y determine el valor del coseno usando una regla milimetrada
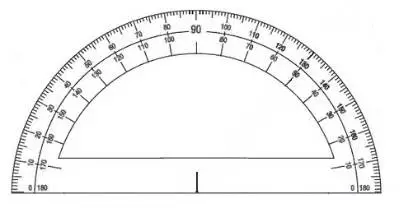
En una hoja cuadriculada dibuje el círculo trigonométrico y usando el transportador represente:
Las razones trigonométricas son una herramienta útil para determinar ángulos sobre objetos físicos.
Ángel Míguez Álvarez