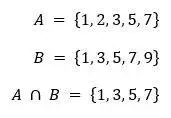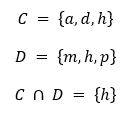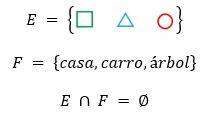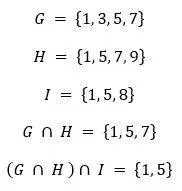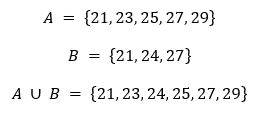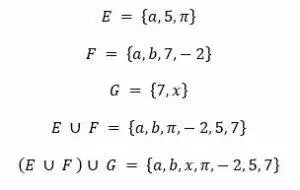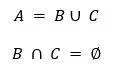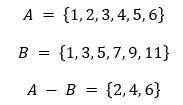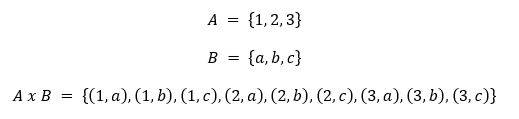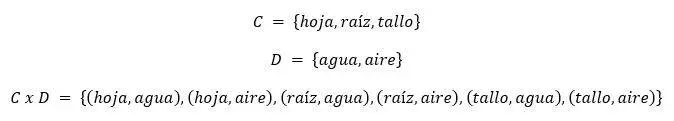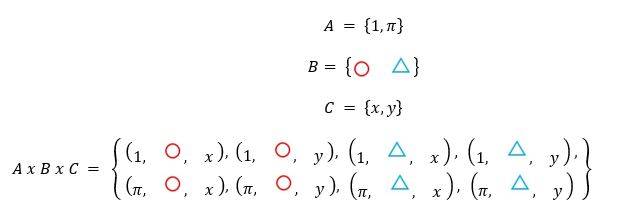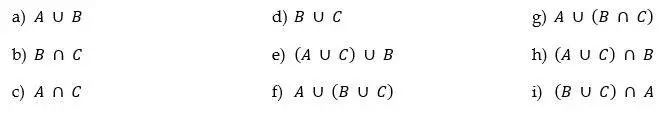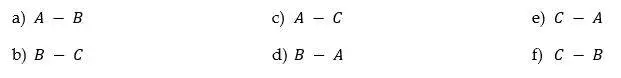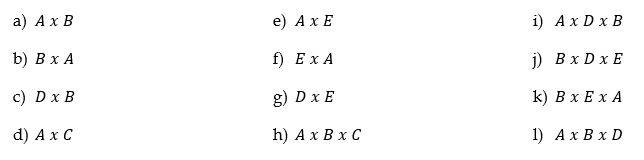Las Operaciones con conjuntos es un proceso mediante el cual obtenemos un nuevo conjunto a partir de dos o más conjuntos.

Ejemplos:
Sea A = {1, 2, 3, 4, 5, 6} y sea B = {2, 4, 6, 8, 10, 12}, hallar A ∩ B

Sea C = {a, b, c, d, e} y sea D = {x, y, z}, hallar C ∪ D

Intersección de conjuntos

La intersección de dos conjuntos A y B es un nuevo conjunto que contiene los elementos comunes al conjunto A y al conjunto B.

Ejemplos:

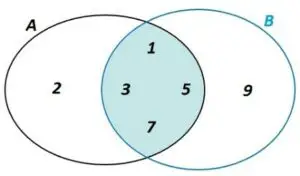
• Sea A el conjunto de todos los números primos de una cifra, sea B el conjunto de todos los números impares de una cifra, hallar el conjunto A ∩ B

fig. 1 A ∩ B

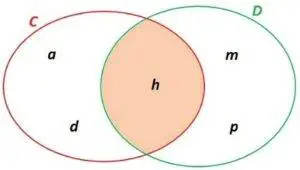
• Sea C = {a,d,h} y sea D = {m,h,p}, hallar el conjunto C ∩ D

fig. 2 C ∩ D

• Sea E = {□, Δ, Ο } y sea F = {casa, carro, árbol}, hallar E ∩ F

fig. 3 E ∩ F = ∅

Cuando la intersección de dos conjuntos es vacía, se dice que ambos conjuntos son disjuntos, por tanto E y F son conjuntos disjuntos.

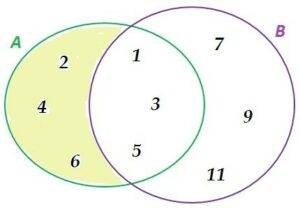
• Sea G = {1,3,5,7}, sea H = {1,5,7,9} e I = {1,5,8} sea hallar el conjunto G ∩ H ∩ I

La intersección de varios conjuntos G ∩ H ∩ I la indicaremos (G ∩ H )∩ I

Por tanto, G ∩ H ∩ I = (G ∩ H )∩ I, esto quiere decir que primero hallamos la intersección del conjunto G con el conjunto H y el conjunto intersección obtenido lo intersectamos con el conjunto I para obtener el conjunto deseado.

fig. 4 G ∩ H ∩ I

Por tanto, G ∩ H ∩ I = {1,5}

Unión de conjuntos

La unión de dos conjuntos A y B es un nuevo conjunto que contiene los elementos del conjunto A, los elementos del conjunto B o los elementos que pertenecen a ambos.

Ejemplos:

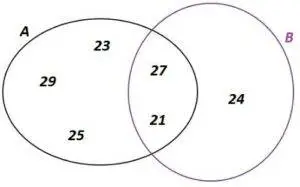
• Sea A el conjunto de los números impares entre 20 y 30, sea B el conjunto de los múltiplos de tres entre 20 y 28, hallar el conjunto A ∪ B

fig. 5 A ∪ B

• Sea C = {a, b, c} y D = {i, x, e}, hallar el conjunto C ∪ D

fig. 6 C ∪ D

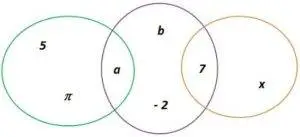
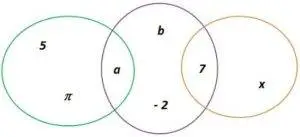
• Sea E = {a, 5, π}, F = {a, b, 7, – 2} y G = {7, x}, hallar el conjunto E ∪ F ∪ G

La unión de varios conjuntos E ∪ F ∪ G la indicaremos (E ∪ F )∪ G

Por tanto, E ∪ F ∪ G= (E ∪ F )∪ G, esto quiere decir que primero hallamos la unión del conjunto E con el conjunto F y el conjunto unión obtenido lo uniremos con el conjunto G para obtener el conjunto deseado.

fig. 7 E ∪ F ∪ G

Partición de un conjunto

Dados varios subconjuntos (B, C, D, E, F) del conjunto A, si los subconjuntos son disjuntos dos a dos, es decir, B ∩ C = ∅, B ∩ D = ∅, B ∩ E = ∅, B ∩ F = ∅, C ∩ D = ∅, C ∩ E = ∅, C ∩ F = ∅, D ∩ E = ∅, D ∩ F = ∅, E ∩ F = ∅ y la unión de todos ellos es el conjunto A, A = B ∪ C ∪ D∪ E ∪ F entonces esos subconjuntos son una partición del conjunto A.

Ejemplos:

• Sea A el conjunto de los integrantes de la banda marcial, sea B el conjunto de los varones que integran dicha banda y C el conjunto de las hembras que también pertenecen a ella. Se cumple lo siguiente:

Entonces, B y C son una partición de A

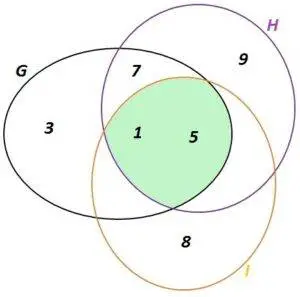
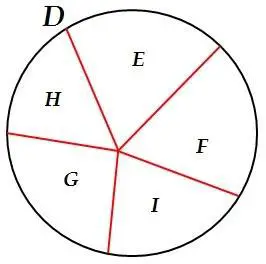
• Sea D el conjunto de los estudiantes de un Liceo, sea E el conjunto de los estudiantes del primer año de ese Liceo, F el conjunto de los estudiantes del segundo año de ese Liceo, G el conjunto de los estudiantes del tercer año de ese Liceo, H el conjunto de los estudiantes del cuarto año de ese Liceo e I el conjunto de los estudiantes del quinto año de ese Liceo.

Tenemos que D = E ∪ F ∪ G ∪ H ∪ I, además E ∩ F = ∅ , E ∩ G = ∅, E ∩ H = ∅, E ∩ I = ∅, F ∩ G = ∅, F ∩ H = ∅, F ∩ I = ∅, G ∩ H = ∅, G ∩ I = ∅, H ∩ I = ∅.

Por tanto, los subconjuntos de D, es decir: E, F, G, H e I son una partición del conjunto D.

fig. 8 partición de D

Diferencia de dos conjuntos

La diferencia entre dos conjuntos A y B (A – B) es el conjunto de los elementos que pertenecen al conjunto A y no pertenecen al conjunto B.

Ejemplo:

• Sea A = {1, 2, 3, 4, 5, 6} y sea B = {1, 3, 5, 7, 9, 11}, hallar el conjunto A – B

fig. 9 A – B

Producto cartesiano de dos conjuntos

Dados los conjuntos A y B se llama producto cartesiano de A por B (A x B) al conjunto formado por todos los pares ordenados de la forma (a, b) tales que a ∈ A y b ∈ B.
El producto cartesiano de conjuntos no es conmutativo.

Ejemplos:

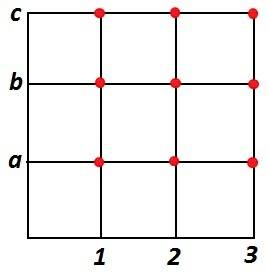
• Sea A = {1, 2, 3} y sea B = {a, b, c}, halle el conjunto A x B

Representación tabular del producto cartesiano de los conjuntos A y B

fig. 10 A x B

• Sea C = {hoja,raíz,tallo} y sea D = {agua,aire}, halle el conjunto C x D

fig. 11 C x D

Producto cartesiano de tres conjuntos

Dados los conjuntos A, B y C se llama producto cartesiano de A por B por C (A x B x C) al conjunto formado por todos las ternas ordenadas de la forma (a,b,c) tales que a ∈ A, b ∈ B y c ∈ C.

El producto cartesiano de conjuntos no es conmutativo.

Ejemplo:

• Sea A = {1,π}, sea B= {Ο, Δ} y sea C = {x, y}, halle el conjunto A x B x C

Ejercicios:

1. Dado los conjuntos: A = {1, 2, 3, 4, 5}, B = {1, 5, 7, 9} y C = {1, 2, 3} hallar los conjuntos:



2. Dados los conjuntos: A = {a, b, c, d, e, f, g, i}, B = {b, d, g, h, j, l, n} y C = {c, f, i, m, o, r, u} hallar los conjuntos:



3. Dado los conjuntos: A = {1, 2, 3, 4, 5}, B = {2, 5, 9} y C = {3, 5, 8, 9} hallar los conjuntos:



4. Dado los conjuntos: A = {1, 3, 5}, B = {2, 7}, C = {0, 3, 5}, D = {2, 3, 5, 7} y E = {4} hallar los conjuntos: