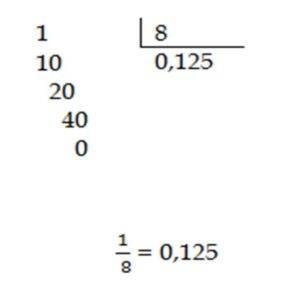Ejemplos de Conversión de Fracciones
La conversión de fracciones es la transformación de una fracción en otra que tenga el mismo valor, pero que tenga un numerador y/o denominador diferente.
- Por ejemplo, si tenemos la fracción 2/4, podemos convertirla en una fracción equivalente que sea más simple, como 1/2. Para hacer esto, dividimos tanto el numerador como el denominador por el mismo número. En este caso, podemos dividir ambos por 2:
2/4 = (2 ÷ 2) / (4 ÷ 2) = 1/2
Por lo tanto, la fracción 2/4 es equivalente a la fracción 1/2.
Cualquier fracción puede ser convertida en una fracción equivalente multiplicando o dividiendo tanto el numerador como el denominador por el mismo número.
- Por ejemplo, si queremos convertir la fracción 3/5 en una fracción con un denominador de 20, podemos multiplicar tanto el numerador como el denominador por 4:
3/5 = (3 x 4) / (5 x 4) = 12/20
Por lo tanto, la fracción 3/5 es equivalente a la fracción 12/20.
Cuando trabajamos con fracciones, podemos simplificarlas para obtener fracciones equivalentes más simples. Además, cuando sumamos o restamos fracciones, necesitamos asegurarnos de que tengan el mismo denominador. Para hacer esto, podemos convertirlas en fracciones equivalentes con el mismo denominador y luego realizar la operación. Para multiplicar o dividir fracciones, simplemente multiplicamos o dividimos los numeradores y los denominadores.
Explicación sencilla
La conversión de fracciones es un proceso matemático que consiste en expresar una fracción en términos equivalentes utilizando diferentes denominadores o numeradores.
La conversión de fracciones es como cambiar un pastel grande en pequeñas rebanadas o pedazos.
- Por ejemplo, si tienes un pastel grande y lo quieres compartir con tus amigos, pero solo tienes un cuchillo pequeño, tendrás que cortar el pastel en pedazos más pequeños para que todos puedan tener un pedazo.
Lo mismo pasa con las fracciones. Cuando queremos compartir algo en partes iguales, como una pizza o una barra de chocolate, podemos usar fracciones. Pero a veces necesitamos cambiar la fracción a otra que tenga un número diferente en el denominador.
Para hacer esto, podemos multiplicar o dividir el numerador y el denominador por el mismo número. De esta forma, tendremos una fracción equivalente que representa la misma cantidad, pero con un número diferente en el denominador.
Ejemplos de Conversión de fracciones
| $$\frac4{-16}=-0,25$$ | $$\frac8{-4}=-2$$ | $$\frac{32}1=32$$ |
| $$-\frac18=-0,125$$ | $$\frac{749}{25}=29,96$$ | $$\frac{1523}{100}=15,23$$ |
Partes de una fracción
Tipos de fracciones
Propias: el numerador es mayor que el denominador.
- Ejemplo de fracciones propias:
| $$\frac4{-16}$$ | $$\frac1{-4}$$ | $$\frac{32}{55}$$ | $$-\frac18$$ |
| $$\frac{749}{2585}$$ | $$\frac{523}{100}$$ | $$-\frac{15}{51}$$ | $$\frac8{17}$$ |
Impropias: el numerador es menor que el denominador.
- Ejemplo de fracciones impropias:
| $$\frac{99}{98}$$ | $$\frac8{-3}$$ | $$\frac{32}1$$ | $$-\frac{12}{51}$$ |
| $$-\frac87$$ | $$\frac{749}{25}$$ | $$\frac{513}{-115}$$ | $$\frac{1523}{100}$$ |
Conversión de fracciones
Pueden hacerse convirtiendo el denominador en la unidad seguida de ceros, mediante fracciones equivalentes.
$$\frac14=\frac{25\times1}{25\times4}=\frac{25}{100}=0,25$$
Ejemplos
$$\frac4{-5}=\frac{2\times4}{2\times-5}=\frac8{-10}=-0,8$$
$$\frac8{-20}=\frac{5\times8}{5\times-20}=\frac{40}{-100}=-0,4$$
$$\frac{749}{125}=\frac{8\times749}{8\times125}=\frac{5992}{1000}=5,992$$
$$\frac{-3}{25}=\frac{4\times-3}{4\times25}=\frac{-12}{100}=-0,12$$
$$\frac{32}{40}=\frac{25\times32}{25\times40}=\frac{800}{1000}=0,8$$
$$\frac{1523}{50}=\frac{2\times1523}{2\times50}=\frac{3046}{100}=30,46$$
Tambien pueden hacerse efectuando la división del numerador entre el denominador
Esto se puede hacer efectuando el algoritmo de la división
Ejemplos
| $$\frac4{-5}=-0,8$$ | $$\frac8{-20}=-0,4$$ | $$\frac{749}{125}=5,992$$ |
| $$\frac{-3}{25}=-0,12$$ | $$\frac{32}{40}=0,8$$ | $$\frac{1523}{50}=30,46$$ |
Así como toda fracción se puede convertir en un número decimal, todo número decimal se puede convertir en una fracción, para ello debes usar el algoritmo de la Fracción Generatriz.La Conversión de fracciones es de gran utilidad cuando se está aprendiendo a ubicar una fracción en la recta real.