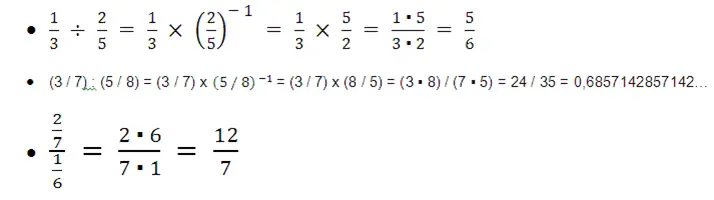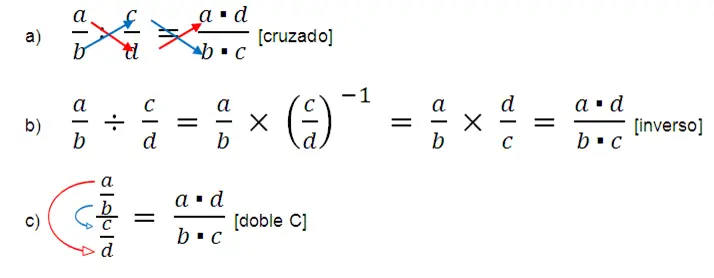La división de fracciones, al igual que todas las divisiones, es equivalente a multiplicar el dividendo por el inverso del divisor.
Ejemplos de división de fracciones:
Procedimientos para dividir fracciones:
Recordemos la división es la operación inversa de la multiplicación. Por tanto realizar una división es equivalente a multiplicar por el inverso del divisor.
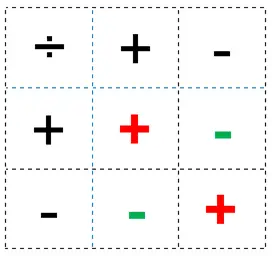
Regla de los signos en la división de fracciones:
En la división la regla de los signos es igual que en la multiplicación
Ejemplos de división de fracciones:
- ( 3 / 5 ) ÷ ( 3 / 2 ) = 6 / 15 = 2 / 5
- ( 7 / 9 ) : = ( 7 / 9 ) ▪ = 14 / 9
- ( – 3 / 5 ) ÷ ( 3 / 5 ) = – 15 / 15 = – 1
- ( 9 / 13 ) : = ( 9 / 13 ) ▪ = 54 / 39 = 18 / 13
- ( 4 / 7 ) ÷ ( 4 / 4 ) = 16 / 28 = 4 / 7
- ( – 6 / 7 ) : = ( – 6 / 7 ) ▪ = – 18 / 7
- ( – 4 / 7 ) ÷ ( 4 / 4 ) = – 16 / 28 = – 4 / 7
- ( 8 / 11 ) : = ( 8 / 11 ) ▪ = 32 / 22 = 16 / 11
- ( – 5 / 9 ) ÷ ( 5 / 2 ) = – 10 / 45 = – 2 / 9
- ( – 7 / 9 ) : ( 2 / 3 ) = ( – 7 / 9 ) ▪ = – 21 / 18 = – 7 / 6
- ( 6 / 11 ) ÷ ( 6 / 8 ) = 48 / 66 = 8 / 11
- ( – 8 / 11 ) : = ( – 8 / 11 ) ▪ = – 32 / 33
- ( – 6 / 11 ) ÷ ( 6 / – 2 ) = 12 / 66 = 2 / 11
- ( 10 / 15 ) : = ( 10 / 15 ) ▪ = 80 / 60 = 4 / 3
- ( 7 / 13 ) ÷ ( 7 / 10 ) = 70 / 91
- ( – 9 / 13 ) : ( 4 / 1 ) = ( – 9 / 13 ) ▪ = – 9 / 52
- ( – 9 / 18 ) ÷ ( 9 / – 11 ) = 99 / 162 = 33 / 54 = 11 / 18
- ( 12 / 19 ) : ( 6 / 12 ) = ( 12 / 19 ) ▪ = 144 / 114 = 1
- ( – 7 / 14 ) ÷ ( 7 / – 5 ) = 35 / 98
- ( – 10 / 16 ) : = ( – 10 / 16 ) ▪ = 20 / 80 = 1 / 4
- ( 8 / 15 ) ÷ ( 8 / 12 ) = 96 / 120 = 4 / 5
- ( – 12 / 20 ) : ( 7 / – 8 ) = ( – 12 / 20 ) ▪ = 96 / 140 = 24 / 35
- ( – 8 / 16 ) ÷ ( 8 / – 8 ) = 64 / 128 = 1 / 2
- ( – 11 / 18 ) : ( 6 / – 5 ) = ( – 11 / 18 ) ▪ = 55 / 108
- ( 9 / 17 ) ÷ ( 9 / 14 ) = 126 / 153 = 42 / 51
- ( 13 / 21 ) : ( 7 / 14 ) = ( 13 / 21 ) ▪ = 182 / 147 = 26 / 21
- ( 5 / 9 ) ÷ ( 5 / 6 ) = 30 / 45 = 2 / 3
En la división de fracciones, al igual que toda división, una fracción es el dividendo y la otra es el divisor.
Ángel Míguez Álvarez
