La Matemática es una ciencia muy valorada, a veces justificadamente y a veces no. De su valoración hay miles de expresiones clásicas entre familias, profesores, académicos y personas de la calle. Es por ello, que han surgido Asociaciones, Comités e Instituciones que promueven competencias en las que se reta a los participantes a resolver problemas matemáticos de variada dificultad.

Hay publicaciones que se han dedicado a difundir esos problemas característicos de las Competencias Matemáticas (Olimpiadas Matemáticas) con la finalidad de ser usados en el entrenamiento, y con frecuencia entretenimiento, de quienes aprecian sus conocimientos y habilidades matemáticas.

Algunas de esas publicaciones las podrás encontrar en la red, por ejemplo: https://librosparaestudiarmatematicas.wordpress.com/2016/10/16/un-desafio-a-la-juventud-ii/.

¿Qué es un problema matemático?

Un tema debatido por infinidad de autores es la definición de lo que es un problema matemático y su diferenciación de un ejercicio matemático, aspecto de gran utilidad para los y las profesoras de matemáticas a la hora de planificar una clase con el fin de abordar la enseñanza de un tópico en particular.

Sobre resolución de problemas se han realizado eventos, escrito tesis, libros y ponencias y en algunos casos se han diseñado programas de formación basados en la resolución de problemas.

Recomendamos leer:

• https://leeryescribirconmat.blogspot.com/2021/10/acerca-de-la-resolucion-de-problemas-en.html
• https://revistas.udea.edu.co/index.php/revistaeyp/issue/view/626.

Ejemplos de problemas Competenciales en Matemática

1. Ejemplo

Si un avestruz pone 2 huevos en 3 días, ¿Cuántos días deben transcurrir para que 4 avestruces pongan 24 de huevos?

Datos:   

1 avestruz →       2 huevos →         3 días

 x avestruces        24 huevos            y días

Plan para resolverlo:   

Tanteo, aumentando un avestruz a la vez y sumando cada 3 días. Observamos que 24 es múltiplo de 2 y de 3 y puedo hallar una proporción

Ejecuto un plan:

Tanteo:

Variando el número de avestruces

1 → 2 huevos → 3 días

4 → 8 huevos → 3 días

Variando también el número de días (se incrementa en ocho el número de huevos cada 3 días)

4 → 16 huevos → 6 días

4 → 24 huevos → 9 días

Verificación de resultados:  Puedo hacer un gráfico

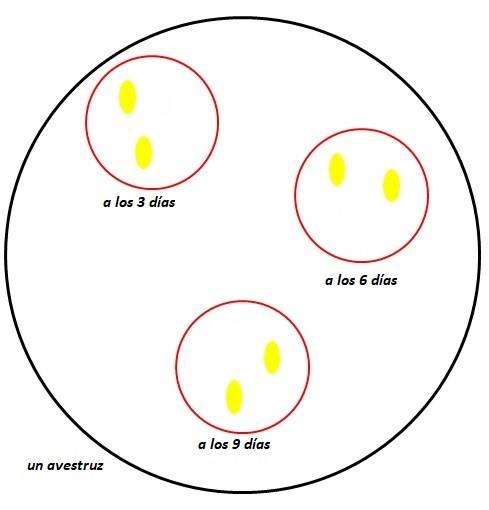fig. 1 N° de huevos en 9 días de un avestruz

Si un avestruz produce 6 huevos cada 9 días, entonces 4 avestruces producirán 24 en el mismo tiempo.

Visión retrospectiva: 

Puedo, a partir de este problema, crear problemas parecidos, con dificultades añadidas.

Supongamos que cada avestruz produce un huevo cada día y medio, ¿cuántos huevos pondrán 8 avestruces en día y medio?

O, si un avestruz y medio, pone un huevo y medio en día y medio ¿cuántos huevos pondrán 3 avestruces en 3 días?

Una práctica que definitivamente desarrolla las habilidades y capacidades de resolver problemas matemáticos es la producción de problemas y luego de resolver un problema, el ambiente puede ser propicio para promover la creación de problemas parecidos al resuelto.

2. Ejemplo:

Si x = 1, y – 10, z = 100 y w = 1000 , calcule:

(x + y + z – w) + (x + y – z + w)  + (x – y + z + w) + (- x + y + z + w)

Datos:

Agrupando

(x + y + z – w) + (x + y – z + w) + (x – y + z + w) + (- x + y + z + w) = (x + x + x – x) + (y – yy + y + y) + (z + z – z + z) + (- w + w + w + w) = 2x + 2y + 2z + 2w

Sustituyendo

(-899) + (911) + (1091) + (1109)

Plan para resolverlo:   

Sustituyo valores y ejecuto la operación de adición o Realizo la operación de adición

Ejecuto un plan:

En los términos agrupados sustituyo los valores y realizo las operaciones indicadas.

2(1) + 2(10) + 2(100) + 2(1000) = 2 + 20 + 200 + 2000  = 2 222

Verificación de los resultados:  

Tomo los valores sustituidos y realizo las operaciones

(-889) + (911) + (1091) + (1109) = 22 + 2 200 =  2 222

Visión retrospectiva:   

La “elegancia” de las respuestas es algo que se valora en las competencias matemáticas. El plan ejecutado demuestra el dominio de las propiedades de la adición, mientras que la verificación de los resultados solo muestra la habilidad para hallar la suma de números.

En un plan de entrenamiento o simplemente en una clase regular deseamos que los estudiantes dominen las propiedades de la adición, dado que las mismas pueden simplificar con creces la realización de operaciones engorrosas.

3. Ejemplo:

Dos números enteros tienen la misma paridad, es decir ambos son pares o ambos son impares. Si tomamos dos números enteros cualesquiera, ¿su suma y su diferencia tendrán la misma paridad?

Datos: 

Si tomamos dos números enteros cualesquiera a y b, puede ocurrir que a = b o que a ≠ b

También puede ocurrir que ambos sean pares, que ambos sean impares o que uno sea par y el otro impar.

Un número entero par es de la forma 2k con k ∈  Z

Un número entero impar es de la forma 2k + 1 con k ∈  Z

Plan para resolverlo:   

debo ejecutar tres procedimientos: primero suponiendo que ambos números enteros son pares; segundo suponiendo que ambos números son impares y por último suponiendo que uno de ellos es par y el otro es impar.

Ejecuto el plan: 

– a =  2k1 y b = 2k2, con k1 y k2 ∈  Z

a + b = 2k1 + 2k2 = 2 (k1 + k2), por tanto, el resultado es par

a – b = 2k1 – 2k2 = 2 (k1 – k2), por tanto, el resultado también es par

De aquí se concluye que si sumo o resto dos números enteros pares el resultado será, en ambos casos, un número entero par.

– a = 2k1 + 1 y b = 2k2 + 1, con k1 y k2 ∈  Z

a + b = (2k1 + 1) + (2k2 + 1) = 2 (k1 + k2 + 1), por tanto, el resultado es par.

a – b = (2k1 + 1) – (2k2 + 1) = 2 (k1 – k2), por tanto, el resultado es par.

De aquí se concluye que si sumo o resto dos números enteros impares el resultado será, en ambos casos, un número entero par.

– a = 2k1 + 1 y b = 2k2, con k1 y k2 ∈  Z

a + b = (2k1 + 1) + 2k2 = 2 (k1 + k2) + 1, por tanto, el resultado es impar

a – b = (2k1 + 1) – 2k2 = 2 (k1 – k2) + 1, por tanto, el resultado es impar

De aquí se concluye que si sumo o resto dos números enteros de distinta paridad el resultado será, en ambos casos, un número entero impar.

Analizando los únicos tres casos a considerar podemos afirmar que al sumar o restar dos números enteros cualesquiera, los resultados obtenidos tendrán siempre la misma paridad.

Verificación de los resultados:  

Hagamos algunos ejemplos concretos y veamos sus resultados.

a = 16 y b = 10,       16 + 10 = 26         16 – 10 = 6 ambos resultados pares

c = 13 y d = 7,         13 + 7 = 20           13 – 7 = 6 ambos resultados pares

e = 15 y f = 8,         15 + 8 = 23           15 – 8 = 7 ambos resultados impares

g = 12 y h = 3,         12 + 3 = 15           12 – 3 = 9 ambos resultados impares

Visión retrospectiva: 

¿Qué sucederá con la paridad de los resultados si multiplicamos o dividimos dos números enteros cualesquiera?

Ejercicios de problemas competenciales

1. Si un avestruz produce un huevo cada día y medio, ¿Cuántos huevos pondrán 8 avestruces en día y medio?
2. Si un avestruz y medio, pone un huevo y medio en día y medio ¿Cuántos huevos pondrán 3 avestruces en 3 días?
3. La suma de una fracción y su inversa es igual a 17⁄4  y la diferencia de ambas es igual a 15⁄4 ¿Cuáles fracciones son?
4. En dos secciones de segundo año presentaron el mismo examen de matemáticas. La primera sección tenía 20 estudiantes y obtuvo una nota promedio de 16 puntos. La otra sección era de 30 estudiantes y su nota promedio en el examen fue de 14 puntos. ¿Cuál sería el promedio de los 50 estudiantes considerados en su conjunto?
5. ¿Un número cuadrado perfecto cualquiera es de la forma 3k + n, con n ∈ Z⁺ ∪ {0} y n < 1?
6. ¿Se puede expresar el número 30 usando tres cifras iguales? (usando los signos de las operaciones)

La aritmética escolar es una parte del currículo matemático que se enseña a los ciudadanos para que comprendan los conjuntos numéricos, sus propiedades, las operaciones válidas en su ámbito de definición y la posibilidad de aplicar estos conocimientos en actividades cotidianas en la vida de cualquier persona instruida.

Ver también:

4. Ejemplos de Múltiplos
5. Ejemplos de Propiedades de la adición
6. Ejemplos de Números Enteros
7. Ejemplos de Números Racionales
8. Ejemplos de Números Primos Relativos
9. Ejemplos de Regla de Tres Simple
10. Ejemplos de Multiplicación de números decimales