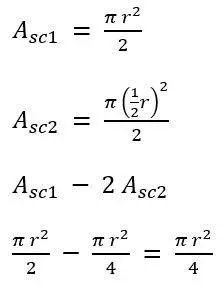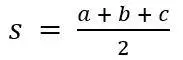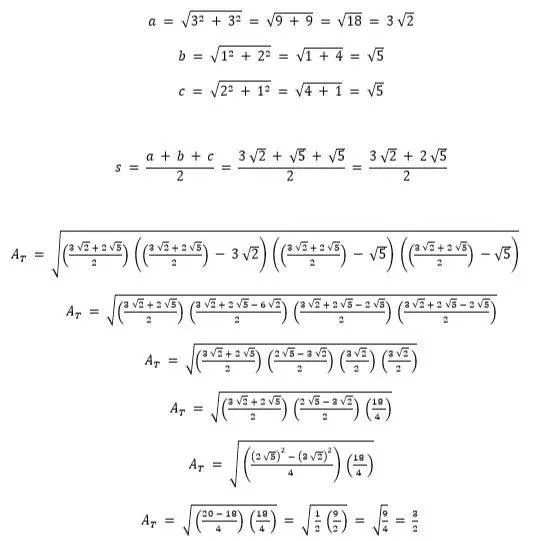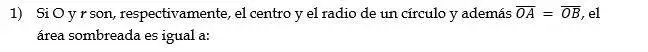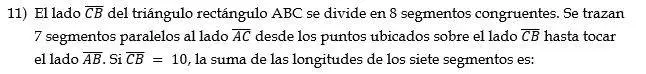¿Qué es un problema geométrico?

Un problema geométrico es una forma que reta la comprensión conceptual, y no solamente los conocimientos de un tema tratado en la actividad de aprendizaje de geometría; exige una reestructuración en la manera de abordar la situación planteada y de los límites de los procedimientos conocidos, y busca generar conexiones sobre conocimientos variados. Un problema geométrico no tiene condición temporal, se puede resolver rápidamente, o no conseguírsele nunca su solución”[1].

¿Cómo se resuelve un problema geométrico?

En 1944 George Pólya escribió un libro donde planteó cómo plantear y resolver problemas[2].

El esquema de resolución que proponemos es este:

• Información que ofrece el problema
• Representación gráfica, comprensión de la dificultad y pasos para resolverlo
• Desarrollo de los pasos para resolverlo
• Verificación de la solución
• Visión retrospectiva

Ejemplos de problemas geométricos Competenciales

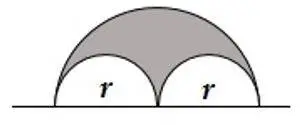
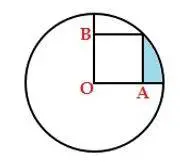
• En la figura 1. ¿Cuál es el área de la región sombreada?

Información que ofrece el problema:   la figura presenta tres semicírculos, uno con longitud del diámetro 2r, y dos con longitud del diámetro r.

Representación gráfica, comprensión de la dificultad y pasos para resolverlo:

fig. 1

• • Calcular el área del semicírculo de radio r
  • Calcular el área de la semicírculo de radio 1/2 r
  • Restarle al área mayor dos veces el área menor

Desarrollo de los pasos para resolverlo:

Verificación de la solución:   el área sombreada equivale al área de un círculo de radio ½ r; es decir, , la cual es la mitad del área del semicírculo de radio r

Visión retrospectiva:    Este problema puede replantearse, en vez de calcular el área sombreada, buscando el perímetro de dicha área definida por tres semicircunferencias.

Uno de los nudos clave en la comprensión de un problema geométrico es el poder descifrar los elementos presentes (en la o las figuras geométricas que ilustran la situación problemática planteada) para determinar los pasos a desarrollar para hallar la solución solicitada.

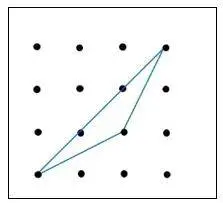
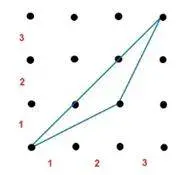
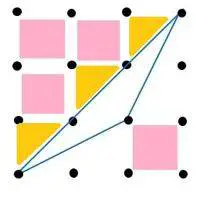
• En la figura 2, las distancias horizontales y verticales entre puntos consecutivos es de 1 centímetro; ¿cuál es el área del triángulo?

fig. 2

Información que ofrece el problema:   la figura presenta un triángulo obtusángulo con ninguno de sus lados en posición vertical ni horizontal. Todos sus lados (triángulo) son la hipotenusa de un triángulo rectángulo formado por los puntos de la cuadricula.fig. 2

Representación gráfica, comprensión de la dificultad y pasos para resolverlo:

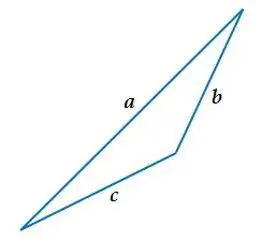
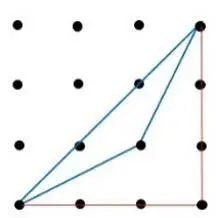
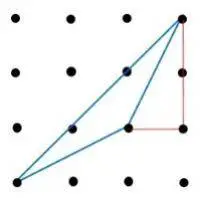
• • Calcular la longitud de cada uno de los lados del triángulo azul usando Pitágoras

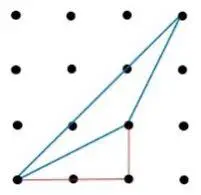fig. 3	fig. 4	fig. 5

• • Calcular el área del triángulo usando la fórmula de Herón

fig. 6

Semisuma de los lados de un triángulo:

Fórmula de Herón:

Desarrollo de los pasos para resolverlo:

Por tanto el área del triángulo azul es 3⁄2 cm² o 1.5 cm²

Verificación de la solución:   la cuadricula que estamos usando como base para graficar el triángulo mide  .

fig. 7

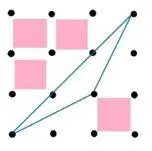
Vamos a ir contando el área no ocupada por el triángulo azul cuadrícula a cuadrícula

fig. 8

El triángulo azul está ubicado dentro de 5 cuadrículas.

Identifiquemos las cuadrículas que están ocupadas por el triángulo azul solo por la mitad.

fig. 9

Podemos señalar, por ahora que el triángulo azul está ubicado en los  no coloreados aun.

Analicemos estos  por partes.

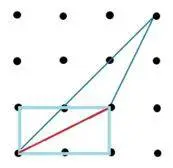
fig. 10

Podemos observar que el rectángulo azul claro abarca 2 cm²  y el lado del triángulo que está dentro del rectángulo lo hemos coloreado de rojo, la línea roja divide el rectángulo por la mitad, a través de una de sus diagonales.

Por tanto, el triángulo azul no ocupa la mitad del área del rectángulo azul claro lo que nos lleva a restarle 1 cm² a los 3.5 cm² que estamos analizando.

Debemos analizar los  que nos faltan.

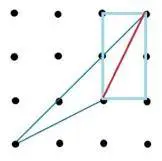
fig. 11

El análisis es análogo al anterior, de los 2 cm² del rectángulo azul claro la línea roja que representa un lado del triángulo azul divide en 2 dicho rectángulo y por ende debemos restar a los 2.5 cm² que nos quedaban 1 cm².

De ahí, que al eliminar todos los espacios no ocupados por el triángulo azul original (figura 7) de los 9 cm² de la cuadrícula están ocupados por triángulo azul solo 1.5 cm².

Lo que nos permite verificar el resultado que habíamos obtenido en el paso anterior.

Visión retrospectiva:    Nos queda aún otras formas de ver este problema. si lo dividimos en dos partes, trazando una perpendicular al lado mayor del triángulo que pase por el vértice opuesto al mismo, obtendremos dos triángulos rectángulos que podemos calcular haciendo uso de teorema de Pitágoras.

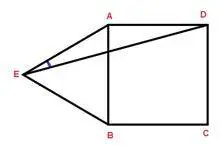
• En la figura 12 ABCD es un cuadrado y ABE es un triángulo equilátero. ¿Cuál es la medida del ángulo ∠AED?

fig. 12

Información que ofrece el problema:   Tenemos una figura compuesta por un cuadrado y un triángulo isósceles.

en el cuadrado todos los ángulos son de 90°

en el triángulo isósceles todos los ángulos son de 60°

tanto en el cuadrado como en el triángulo isósceles todos los lados son de igual tamaño.

Representación gráfica, comprensión de la dificultad y pasos para resolverlo:

• • Tenemos el triángulo ADE y debemos hallar el valor del ∠AED
  • Debemos establecer la relación entre los lados del triángulo ABE y el cuadrado ADCB
  • Igualmente, debemos establecer las relaciones entre los ángulos en el triángulo ADE

Desarrollo de los pasos para resolverlo:

fig. 13

Podemos establecer en el cuadrado que:

igualmente en el triángulo tenemos que:

de donde se concluye que: .

Por tanto el triángulo ADE es isósceles y por tanto el ∠AED = ∠ADE

Adicionalmente el ∠EAD = 90° + 60°, por ser la suma de los ángulos internos de un cuadrado y de un triángulo isósceles.

∠EAD = 150° Þ ∠AED = 15°

Verificación de la solución:   una solución gráfica es cuántas veces cabe el ∠AED en el ∠ADC

Visión retrospectiva:    En geometría, los problemas, tienen una fuerte presencia de las imágenes, más debemos rigurosamente demostrarlos algebraicamente con base en los conceptos, definiciones y razonamientos deductivos.

Ejercicios:

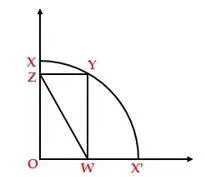
fig. 14

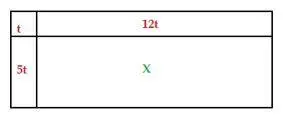
fig. 15

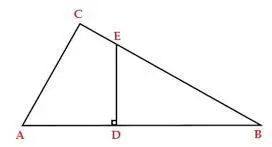
fig. 16

fig. 17

fig. 18

fig. 19

fig. 20

La geometría es una parte del currículo matemático que se enseña a los ciudadanos para que comprendan las formas, sus dimensiones, las relaciones entre sus componentes y la posibilidad de aplicar estos conocimientos en actividades cotidianas o hechos presentes en la vida de cualquier persona instruida.

Para profundizar sobre problemas competenciales te sugerimos revisar este libro: https://librosparaestudiarmatematicas.wordpress.com/2016/10/16/un-desafio-a-la-juventud-ii/

Ver también

• Ejemplos de ángulo agudo, obtuso, llano y recto
• Ejemplos de Ángulos en la circunferencia
• Ejemplos de Áreas de Cuerpos Geométricos
• Ejemplos de Cilindros para Niños
• Ejemplos de cómo calcular el área de un polígono irregular
• Ejemplos de cómo sacar el área de un Triángulo
• Ejemplos de cómo sacar los metros cuadrados
• Ejemplos de Cuadriláteros: Trapecios, Paralelogramos y Trapezoides
• Ejemplos de líneas y puntos notables de un Triangulo
• Ejemplos de Volumen y Áreas de Pirámides

Ángel Míguez Álvarez

[1]       Míguez, Á. (2 003) “Caracterización de los ejemplos, ejercicios, problemas y preguntas usados en el aula, en los libros de texto y demás materiales escritos de matemática en el contexto escolar venezolano”. En: Revista Educación y Pedagogía. Medellín: Universidad de Antioquia, Facultad de Educación. Vol. XV, No. 35, (enero-abril).

[2]       Polya, G. (1 969). Cómo plantear y resolver problemas. México: Trillas.